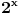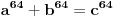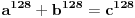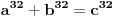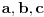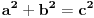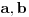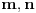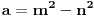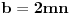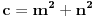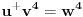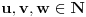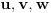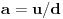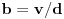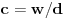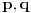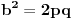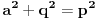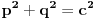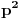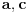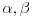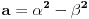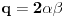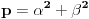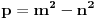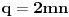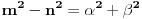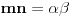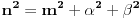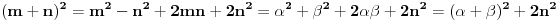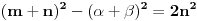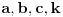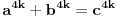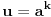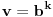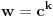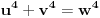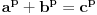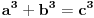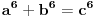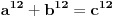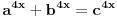fermatova poslednja teorema ima oblik
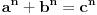 , i tvrdi da ne postoje celi pozitivni brojevi a, b, i c, gde je stepen veci od 2.
, i tvrdi da ne postoje celi pozitivni brojevi a, b, i c, gde je stepen veci od 2.uzmemo da je stepen 4.
prvo, krecemo od pitagorine teoreme.
ona uvek ima oblik
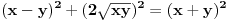 , a takodje obratno, sve sto ima ovakav oblik potpada pod pitagorinu teoremu.
, a takodje obratno, sve sto ima ovakav oblik potpada pod pitagorinu teoremu.kada ovo kvadriramo, dobijamo
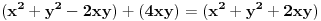 . zagrade sam stavio samo da se lakse uoce clanovi.
. zagrade sam stavio samo da se lakse uoce clanovi.ako sada ovo takodje zelimo da kvadriramo (svaki clan ponaosob) da bi dobili cetvrti stepen onih pocetnih clanova, onda ovi sadasnji clanovi takodje moraju imati neki oblik
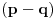 i
i 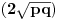 i
i 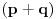 jer prakticno opet radimo pitagorinu teoremu.
jer prakticno opet radimo pitagorinu teoremu.kada pogledamo ono gore kvadrirano, onda bi mogli privremeno da zamenimo da je
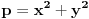
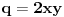
za te vrednosti drugi clan (ili srednji clan, ili b) bi onda morao da ima oblik
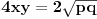 .
. iz ovoga izvlacimo (kada zamenimo p i q) da je drugi clan u kvadriranom izrazu
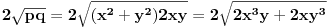
dakle, dobijamo da bi, ako je cetvrti stepen moguc, za srednji clan trebala vaziti jednakost
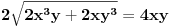
ovo se moze sve podeliti sa 2, i dobijamo
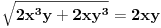 . kvadriramo levu i desnu stranu i imamo
. kvadriramo levu i desnu stranu i imamo 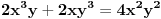
sve mozemo podeliti sa 2xy i dobijamo
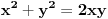
to se onda moze napisati kao
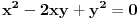
ova jednakost je tacna za cele brojeve a i b, jedina stvar koja nije u redu je da je resenje: a je uvek jednako b! ako je a=b, to nas vraca na pocetnu postavku u kojoj je prvi clan (a-b), a samim tim taj clan ne bi postojao, niti izraz za pitagorinu teoremu na osnovu koje smo izvukli ovaj izraz za fermatovu teoremu za cetvrti stepen.
time se izvodi zakljucak da ne moze postojati fermatov izraz za oblik
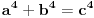 tj za stepen koji je jednak 4.
tj za stepen koji je jednak 4.isti postupak je dalje za n=8, 16, 32, 64... al mrzi me sad da racunam.
probao sam da izvucem opsti dokaz za sve 2^n, al sam blokirao od svih ovih brojki i slova, pa mozda nekad, ako je ovo tacno. al skontao sam da ako se moze uopstiti na 2^n, pa odatle na sve parne stepene, onda je cela feramtova teorema dokazana.
al u ovom slucaju...valjda je to to?
[Ovu poruku je menjao number42 dana 09.06.2013. u 18:58 GMT+1]




 dokaz fermata za n=4, 8, 16, 32, itd...?
dokaz fermata za n=4, 8, 16, 32, itd...?