Neka je
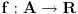
i
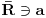
tačka nagomilavanja skupa
.
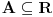
Treba da pokažemo da ako (po
Heine-u) za svaki realni niz
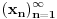
, (takav da
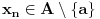
i
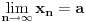
) važi
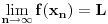
, onda važi i
.
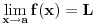
Izgleda da je uobičajen dokaz kontrapozicijom tj. da iz
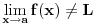
sledi da postoji niz koji ispunjava sve navedene uslove, ali za koga
ne važi .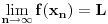
Pretpostavimo da je
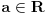
(za
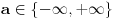
dokaz ostaje potpuno isti samo se pripadnost tačke
okolini tačke
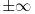
iskazuje neznatno drugačije - pa bi zapis preko okolina bio sažetiji - ali kad smo već krenuli ovako...
)
Prisetimo se da
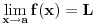
u stvari znači da
.
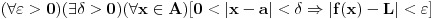
Dakle, iz
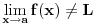
sledi da
postoji neko
takvo da
za svako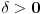 
postoji
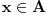
za koje važi
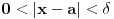
ali za koje
ne važi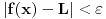 
nego
.
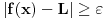
Pošto to važi za
svako 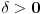, onda uzimajući redom da je
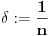
dobijamo niz tačaka
za koje važi
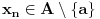
i
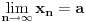
ali za koje očigledno
ne važi .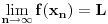
Ajde, da probam sad to isto ali bez kontrapozicije. Neka je
skup svih realnih nizova
koji ispunjavaju one
Heine-ove uslove i neka je
.
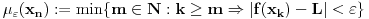
Neka je
proizvoljno i
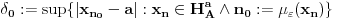
, pa ako stavimo
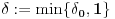
, onda za svako
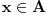
za koje važi
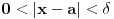
, postoji neki niz
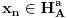
i postoji
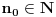
tako da važi
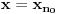
, pa samim tim i
.
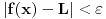
Neke očigledne stvari nisam posebno obrazložio ali, ako bude potrebno, rado ću to učiniti.
[Ovu poruku je menjao uranium dana 10.02.2006. u 00:16 GMT+1]
Attempt all the problems. Those you can do, don't do. Do the ones you cannot.
dokaz ekvivalentnosti definicija limesa po Cauchyu i Heineu?
