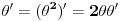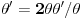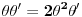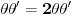Citat:
petarm: Vidis matematika sama za sebe bas i nema smisla. Da nigde nije nasla primenu ne bi ni postojala. Ti recimo u kvantnoj fizici mozes da definises potencijal kao
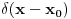
... Itd. Za ovakve probleme iz prakse ova definicija radi.
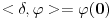
Sa ovim stavom se ne bih složio, ali nema potrebe da o tome ovde polemišemo jer to zalazi u filozofiju i nema veze sa ovom temom.
Citat:
petarm: Za ovakve probleme iz prakse ova definicija radi.
E, pa vidiš, za probleme kao što je ovaj o kome se diskutuje na ovoj temi ne radi. Matematika ti daje aparat u koji ćeš moći da se pouzdaš u svim njegovim interpretacijama, uz jedini uslov da se strogo pridržavaš pravila. Pa, pridržavaj ih se ili nemoj postavljati pitanja kao što je ono iz prve poruke na ovoj temi, jer ti matematika onda ništa i ne garantuje.
Citat:
petarm: Da i zaboravio si da joj je u originalnoj definiciji u data vrednost
.
Nisam ništa zaboravio, niti znam da li je taj uslov uključen u originalnu Dirakovu definiciju. Uslov koji "Dirakovoj funkciji" daje beskonačnost u nuli glasi
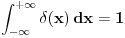
, obzirom da je
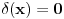
za
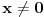
. No, to je sve besmisleno u Lebegovom zasnivanju integralnog računa.
Drugim rečima, taj uslov ne menja ništa. Neka je
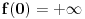
i
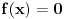
za
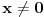
. Ako sa
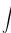
označimo Lebegov integral, biće
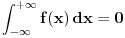
. Obnovi Lebegov integral. Njegova vrednost se ne menja promenom vrednosti podintegralne funkcije u jednoj tački, makar ta vrednost bila i
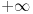
. Ako je
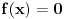
svuda osim eventualno u jednoj tački, onda je svakako
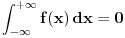
bez obzira na vrednost
u toj jednoj tački, bila ona konačna ili beskonačna.
Citat:
petarm: Ja ne brinem bas toliko da li je nesto formalno dobro definisano ako mi to ne pravi nekih vecih problema. Ne trazim bas dlake u svakom problemu...U nekima da.
Zato i imaš problema kao što je onaj sa početka teme.
Citat:
petarm:
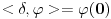
Mozes to i ovako zapisati
.
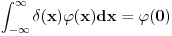
Samo ako uvedeš novu teoriju integracije u kojoj to može da prođe. U Lebegovoj jok. Ne može se u matematici samo mućkati izrazima bez vođenja računa o njihovom značenju. Ja simbol
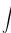
interpretiram kao Lebegov integral i tu ovo što si napisao ne prolazi. Ako imaš neku drugu definiciju integrala, navedi je, pa da vidimo.
Citat:
petarm: Sta mislis o ovom definiciji
funkcije?
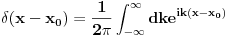
Ako se misli na Lebegov integral, besmislena je. Ako ne, onda je nepotpuna, jer joj fali značenje simbola
.
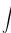
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
Dokaz da je 1=2?
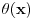- Hevisajdova fja 
