Citat:
barum:
Da li te transformacije nad dužima mogu da dovedu do toga da M i N ne moraju da budu različite tačke?
Ne. Tačke
i
određuju pomenute duži, i na te tačke ne možeš uticati — takve su kakve su. E sad, kad dobiješ duži, onda ih možeš „iščupati“ iz tetraedra i negde sa strane od njih formirati trougao.
Citat:
barum:
Da li to znači da iako je rečeno da M pripada ABC "kraju stola" ne mora tu i da ostane već je slobodno?
Vidi gore.
Citat:
barum:
Sada vidim da zadatka nije ni bilo.
Razni ljudi su se već uveliko uključilo u rešavanje zadatka (bata kg je ponudio jedno rešenje pa sad ispitujemo je li korektno, i zzzz razmatra jedan pristup, a još je odavno qzqzqz rešio nešto slično, samo u dve dimenzije), pa ova tvoja izjava da „zadatka nije ni bilo“ ne deluje baš smisleno (a ni kulturno prema tim ljudima).
Citat:
zzzz:
Znači li to da:
Od navedenih stranica se uvjek može sklopiti trougao. A tačke M i N mogu
ležati čak i izvan tetraedra u odgovarajućoj ravni? Citat:
zzzz:
Mislim da bi rješavanje išlo preko vektora, zatvaranjem poligona pomoću ivica tetraedra, AB,BC,CD.
Jesam li zalutao?
Rešenje koje ja imam ne koristi vektore. Zapravo, imam dva rešenja, od koje je jedno ono „apstraktno“ iz naslova, dok je drugo prizemnije(i dosadnije); nebitno, nijedno od njih ne koriste vektore. No, to svakako ne znači da je nemoguće rešiti zadatak preko vektora — probaj, pa ako uspeš, super.
Ljubičice crvena, što si plava kô zelena trava.
[Zadatak]: Nešto potpuno apstraktno
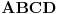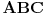pravilan tetraedar i 
i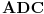 
, redom. Pokazati da su duž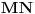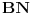i 
, 
i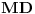 
stranice nekog trougla.
Registrovani: 3 ( Nebojsa Milanovic, Ultrena, Miroslav Cvejić )
Re: [Zadatak]: Nešto potpuno apstraktno
Doduše, pojavi se ponekad na forumu i pokoji otvoren problem (tj. „zadatak“ koji dosad niko na svetu nije rešio), ali ovaj nije takav — uopšteno, za zadatke koje ja postavim uvek imam rešenje, ako nisam naglasio suprotno (ali kad nema interesovanja ni ja ne žurim s objavljivanjem, kako bih nekom ko se možda kasnije zainteresuje dao priliku da sam pokuša).
