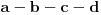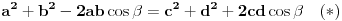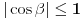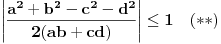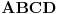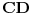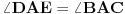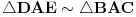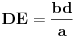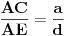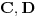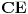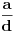Citat:
Farenhajt:
Da li za SVAKU takvu četvorku UVEK postoji četvorougao čije su to stranice (ne obavezno u cirkularnom redosledu a-b-c-d, nego u bilo kom), a koji je tetivan?
Postoji, i pri tom možemo i fiksirati redosled stranica. Neka je redosled, recimo,
.
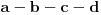
Povlačeći dijagonalu, lako se utvrđuje da mora važiti
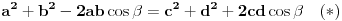
, gde je
ugao između
i
(a onda je
ugao između drugih dveju stranica). Kako mora biti
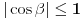
, iz rečenog se lako izvodi uslov
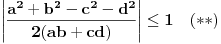
, a nije teško proveriti kako je ovo u stvari ekvivalentno tvrdnji da je svaka stranica manja od zbira ostalih triju. S druge strane, imajući
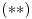
, može se na osnovu
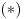
konstruisati dijagonala, a onda je sve gotovo (konstrukcija je pomalo naporna, ali sasvim pravolinijska).
E sad, sama konstrukcija se može izvesti i lakše, ali onda je diskusija malo zamagljenija. No, pošto smo diskusiju već obavili, priložiću i pomenutu konstrukciju (reč je o konstrukciji Šturma).
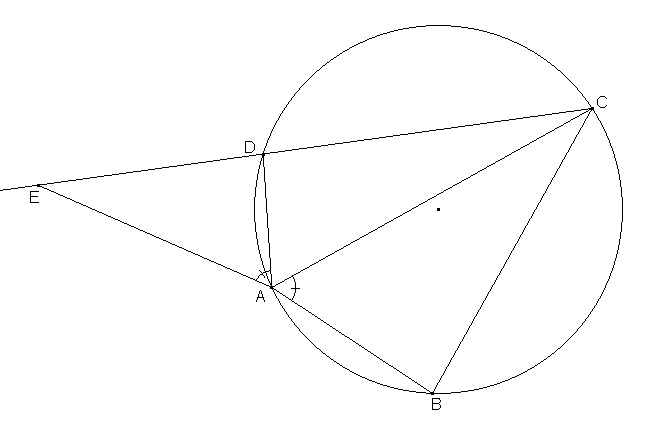
Neka je
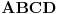
traženi četvorougao. Odaberimo na produžetku stranice
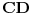
preko
tačku
takvu da je
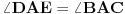
. Sada važi
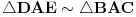
, pa je
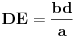
. Iz iste sličnosti dobijamo i
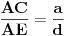
. Dakle, konstrukciju sprovodimo na sledeći način: odredimo tačke
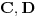
i
, tačku
nađemo u preseku Apolonijeve kružnice nad duži
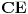
za odnos
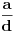
i kružnice sa centrom u
, poluprečnika
, i to je to.
Ljubičice crvena, što si plava kô zelena trava.
Zadatak o diskusiji konstruktibilnosti
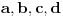koja zadovoljava neophodan uslov da ti brojevi budu stranice četvorougla - naime, da je zbir svaka tri strogo veći od četvrtog.