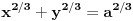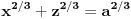Da li ti je inače jasan princip po kome se, u dve dimenzije, izračunava površina ispod grafika neke funkcije? Razlaganje na elementarne pravougaonike, sumiranje, i uzimanje limesa koji se onda definiše kao integral?
Kod zapremine je potpuno isti princip, samo što umesto pravougaonika, dimenzija
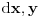
, uzimamo elementarnu prizmu dimenzija
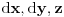
. U opštem slučaju, pošto imamo dva diferencijala, rešavanje će zahtevati dvostruki integral. Međutim, u ovom konkretnom slučaju stvar se svodi na jednostruki, zbog geometrijskih osobina cilindra, a za to pojednostavljenje dobro prouči moj post u kome navodim postupak i konačni rezultat, pa priupitaj ako ti šta ostane nejasno.
Možeš i pažljivo razgledati sliku koju si napravio: Geometrijsko telo je nekakav "piramidoid" (ovaj termin ne postoji) čija baza leži u ravni
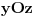
, tako da ga možeš rastavljati na slojeve - preseci ga proizvoljnom ravni
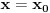
i na tom preseku podigni elementarnu prizmu debljine
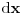
. Postavi izraz za površinu tog preseka u zavisnosti od

- označimo je sa
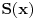
- a onda integrali
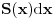
(što je zapremina elementarne prizme čija je baza
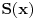
a visina
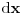
) u odgovarajućim granicama.