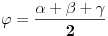Pa, imam samo malčice humanije rešenje. Pre svega, i dalje ostaje da se "peške" dokaže da je

. Međutim, ostala računica može se donekle uprostiti ako se uzme u obzir sledeće: Ukoliko se jedna bočna ivica neke trostrane piramide produži

puta, a druge dve ostanu nepromenjene, zapremina će se povećati

puta - što je očigledno ako se za bazu uzme trougao određen dvema nepromenjenim bočnim ivicama. Dakle, dokaže li se stav za
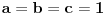
, dokazan je uopšte. Stoga analitički pristup postaje malo lakši: Uzmimo tačke
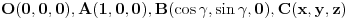
i postavimo uslove preko intenziteta i skalarnih proizvoda:
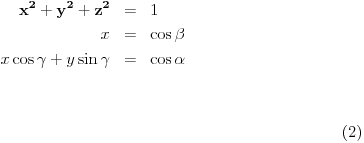
i čini mi se da se računica donekle pojednostavljuje jer se onda visina direktno dobija kao

, a površina baze je, jasno,
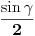
.
Dodatak: Ni ona trigonometrijska formula nije odveć komplikovana za dokaz - dovoljno je dvaput transformisati proizvod u zbir, i posle toga se uglavnom sve lepo sredi.
[Ovu poruku je menjao Farenhajt dana 30.08.2006. u 17:18 GMT+1]
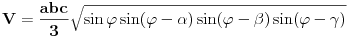
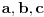 dužine bočnih ivica;
dužine bočnih ivica; 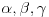 uglovi među bočnim ivicama;
uglovi među bočnim ivicama;