Prvi zadatak je stvarno lak, štaviše može da se reši i sa
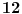
kuglica (zapravo, Safet Beriša je
ovde rešio jednu varijantu ali na osnovu njegovog rešenja ne možemo reći da li je lažna kuglica teža ili lakša od ostalih). Osim toga, umesto uslova "jedna je deformisana" ništa se ne menja ni ako kažemo "najviše jedna je deformisana".
Neka su kuglice obeležene slovima
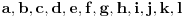
. U
prvom merenju upoređujemo kuglice
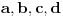
sa

. Ako nijedna strana ne preteže u
drugom merenju upoređujemo kuglice
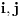
sa
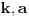
. Ako su terazije ponovo u ravnoteži u
trećem merenju upoređujemo

sa

. Ako je nastala ravnoteža sve kuglice su jednake (dodatni uslov zadatka), ako

preteže onda je ona lažna i teža, a ako

preteže onda je

lažna i lakša. Pretpostavimo sada da u drugom merenju preteže strana
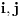
(potpuno isto se radi i u slučaju da je ta strana lakša). U
trećem merenju upoređujemo
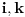
sa
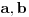
. Ako su jednake lažna i teža je
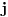
, ako
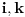
pretežu lažna i teža je

, ako su
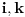
lakše od
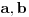
onda je

lažna i lakša.
Pretpostavimo sada da su su u prvom merenju pretegle
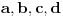
(opet je svejedno koja strana preteže jer se radi potpuno isto). U
drugom merenju upoređujemo
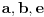
sa
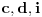
. Ukoliko su jednake u
trećem merenju upoređujemo

sa

. Ako su jednake lažna i lakša je
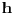
, u suprotnom je lažna ona koja je lakša (i lakša je od svih ostalih). Ako u drugom merenju pretegne strana
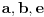
onda u
trećem merenju upoređujemo

sa

i ako

pretegne onda je ona lažna i teža od ostalih, dok je u slučaju ravnoteže

lažna i teža (možemo zapaziti i to da je nemoguće da

pretegne u ovom merenju). Preostao je još slučaj kada je
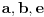
lakše od
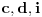
. Tada u
trećem merenju upoređujemo
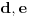
sa
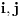
. Ako je
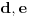
lakše onda je lažna i lakša

, ako je teže onda je lažna i teža

, dok je u slučaju ravnoteže lažna i teža kuglica

.
To bi bio kraj prvog zadatka (tačnije, nešto opštije verzije). Sada da se pozabavimo drugim.
Pošto ovde nema toliko mnogo permutacija neću obeležavati slovima da ne bih bespotrebno komplikovao. U
prvom merenju uporedimo četiri kuglice sa druge četiri. Ukoliko jedna strana preteže dalje nastavljamo potpuno isto kao u prethodnom zadatku. Pretpostavimo zato da su terazije u ravnoteži, što znači da je lažna kuglica među preostalih pet. Uzmimo tri od njih i u
drugom merenju ih uporedimo sa tri ispravne (iz one grupe koju smo koristili u prvom merenju). Ukoliko pretežu (analogno ako su lakše) u
trećem merenju međusobno uporedimo dve od njih i ako su u ravnoteži lažna i teža je preostala, dok u suprotnom lažna i teža je ona koja pretegne. Preostaje još slućaj da su u drugom merenju terazije u ravnoteži, što znači da je lažna kuglica jedna od preostale dve. Uzmimo jednu od te dve i u
trećem merenju je uporedimo sa jednom ispravnom. Ukoliko je teža/lakša znamo da je ta kuglica lažna i teža/lakša od ostalih, dok u slučaju ravnoteže znamo da je lažna preostala kuglica, ali
ne znamo da li je teža ili lakša od ostalih.
Kad smo već ovde postavlja se pitanje možemo li poboljšati način merenja tako da na kraju saznamo i da li je lažna kuglica teža ili lakša. Odgovor je ne, i to ćemo upravo dokazati. U svakom merenju može da se dogodi jedan od tri slučaja (leva strana preteže, desna strana preteže, ili ravnoteža), što znači da iz dva merenja možemo razlikovati najviše
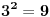
situacija. Ako smo u prvom merenju na tasove stavili po
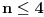
kuglice pretpostavimo da su terazije u ravnoteži. Dakle, lažna kuglica je među preostalih bar pet i kako može biti ili teža ili lakša od ostalih to nam daje ukupno bar deset mogućnosti, a sa preostala dva merenja možemo da "pokrijemo" najviše devet. Slično, ako u prvo merenju stavimo po
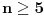
kuglica pretpostavimo da jedna strana preteže. Tada lažna kuglica može biti teža na težem tasu ili lakša na lakšem tasu, pa pošto imamo bar deset kuglica na terazijama imamo i bar toliko mogućnosti, i time smo opet došli do kontradikcije.
Što se tiče uopštenja problema na adresi
www.cs.cmu.edu/afs/cs/academic...w/lecture-notes/coincompet.pdf postoji jedan dokument vezan za to, iako se radi pretežno o teorijskoj priči možda će nekog zainteresovati.
Ljubičice crvena, što si plava kô zelena trava.