Nije fazon nalaziti rešene primere, pa postavljati ovde, podseća me na voditeljke/voditelje u kvizovima, kad se prave pametni čitajući odgovore na pitanja na koja niko od tamičara nije dao tačan odgovor, pa ispadaju ne znam koliko pametniji od tih takmičara.
Sa druge strane, naš obrazovni sistem je malo....
Sećam se zadatka sa nekom zapadnog univerziteta, SAD ili Kanada, gde se već u prvom semestru uči gama funkcija, ali samo osnovne osobine, potom odmah diferencijalne jednačine, opet najosnovnije, pa se kasnije uče neke teže stvari u narednim semestrima.
Sećam se zadatka sa jednog takvog kursa:
Ne znajući za postojanje trigonometrijskih funkcija, diskutovati rešenja diferencijalne jednačine y'' + y = 0.
Da li bi taj "zadačić" znali da reše čak i oni koji kod nas diplomiraju matematiku je neko drugo pitanje, nije do sposobnosti i znanja, već se ovde i dalje forsira "ruska škola", koja ima potpuno drugačiji pristup, koji je možda dobar za one naj-naj-najbolje, ali nije dobar za one koji su malo ispod njih, o prosečnima da ne govorimo, a tek o primeni u privredi bolje ne pričati.
Sećam se i zadatka tipa "naći bar jednu funkciju f(x) koja je nenegativna na intervalu [0, +∞), nema limes u +∞, a njen određen integral na tom intervalu ima konačnu vrednost" (što će reći da je površina između grafika te funkcije i x-ose konačna).
Sreća da sam nekako "slučajno" povezao jedan primer iz telekomunikacija sa nekim primerom reda iz matematike čija je vrednost (π^2)/6, pa konstruisao jednu takvu funkciju :)
Donekle forsiranje učenja napamet i rešavanja tipskih zadataka koji na prvi pogled nigde nemaju primenu je jedan od krivaca zašto naši diplomci imaju kasnije problem sa "out of the box" razmišljanjem, inoviranjem rešenja, itd.
Blessed are those who can laugh at themselves, for they shall never cease to be amused.
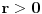 takvo da postoje neprekidne funkcije
takvo da postoje neprekidne funkcije 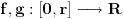 diferencijabilne na
diferencijabilne na 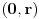 takve da važi sledeće:
takve da važi sledeće: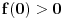 ,
, 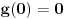 ,
, 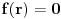 ,
,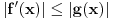 ,
, 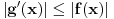 za
za 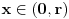 .
.