Bojan je dao dobru ideju, mislim da važi činjenica da je npr. PQ + HQ minimalno kada su PCQ i AHQ slični.
Sećam se prošlogodišnjeg zadatka sa primenom na ETF-u, nešto tipa iz tačke (2,3) i (3,5) se povuku duži do tačke M između 2 i 3 na x-osi, naći položaj tačke M tako da zbir duži iz date 2 tačke do tačke M bude minimalna - rešenje je takvo da te duži sa visinama iz datih tačaka na x-osu i delovima x-ose grade slične trouglove - to je problem konopca vezanog krajevima za vrhove stubova različite visine koji dodiruje tlo, minimalna dužina se dobija u tački koja je teme sličnih trouglova (stubovi, linije na tlu od tačke dodira konpoca sa tlom i stubova, i samog konopca).
Nisam imao vremena da proveravam dokaz ovoga, ali su i ovi na ETF-u valjda računali na poznavanje tog problema, pa se dati zadatak onda rešava brzo. Ako se krene sa izvodima i sl., brzo se pogubi u računu, i mislim da se to rešava pomoću nejednakosti, gde je granični slučaj jednakost, ali sam zaboravio koju nejednakost treba primeniti.
Dakle, rešenje bi trebalo da bude da je trougao PCQ bude sličan trouglu ABC.
Međutim, to važi kada jedna od tačaka P i Q fiksirana.
Problem je što, ako zadržimo princip, a pomeramo obe tačke P i Q, dobijamo praktično da je P = Q = C, a K = H, čime se u stvari i dobija ekstrem za funkciju koju je odredio miki (ispod nacrtanog trougla, na strani 2, zaokruženo rešenje u zadatku dobija se za x=a, y=b, samo pošto je c nepoznato, u rešenju su umesto c napisali koren iz a^2+b^2).
Da li je minimum slučaj kada je P=Q=C ili kada je Q=A, može lako da se proveri, pa ću preći na sledeći slučaj.
Drugi slučaj, kada je trougao PCQ kao lik u ogledalu u odnosu na prethodni slučaj trougla PCQ, ima dva ekstrema - ono koje je već prethodno dobijeno, i drugo za koje važi P=B=K, Q=A=H. U tom slučaju, zbir datih duži je jednak c, pa treba proveriti da li je to veće ili manje od prethodno dobijenog rešenja.
Dakle, pretpostavimo da je prvo dobijeno rešenje minimum, tada je:
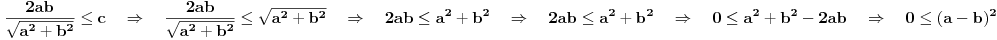
što je uvek tačno!
Blessed are those who can laugh at themselves, for they shall never cease to be amused.