Hteo sam sinoć da napišem nešto slično, ali hajde da dopunim. Negde sam to pisao na ovom forumu, ali je teže naći jer se tema ne zove tako.
Elem,
Pod potpoljem od

podrazumevaćemo bilo koji podskup

od

takav da 0 i 1 pripadaju tom podskupu i da ako su
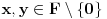
, onda i
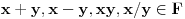
. Najmanji takav skup je

. Međutim, ako je

bilo koje potpolje od

i

neki njegov pozitivan element, onda je i
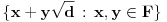
potpolje od

.
Neka su

i

dva potpolja od

i neka je
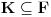
. Tada je

jedan vektorski prostor nad poljem

. To znači da važe uobičajeni zakoni vezani za sabiranje i oduzimanje vektora i množenje vektora skalarom, kao u geometriji, s tim da su ovde skalari elementi skupa

, a vektori elementi skupa

.
Ako je pritom

neki niz vektora takav da za ma koji vektor

postoji tačno jedan niz skalara

tako da važi
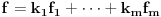
, onda za niz vektora

kažemo da je baza vektorskog prostora

nad poljem skalara

.
Pritom se dokazuje da svake dve baze istog vektorskog prostora nad istim poljem skalara imaju isti broj elemenata. Drugim rečima, ne postoje baze

i

istog vektorskog prostora nad istim poljem skalara takve da je
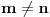
.
Broj elemenata bilo koje baze vektorskog prostora

nad poljem skalara

se zove dimenzija vektorskog

nad poljem skalara

. U slučaju da je vektorski prostor neko polje, a polje skalara njegovo potpolje (kao kod nas), taj broj se obeležava sa
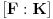
Ukoliko je

potpolje od

a

potpolje od

, onda važi formula
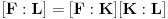
.
Neka je

neko potpolje od

i

bilo koji kompleksan broj. Najmanje potpolje od

koje sadrži sve elemente polja

, kao i

uvek postoji i obeležava se sa
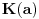
.
Ukoliko ne postoji nijedan ne/nula polinom

sa koeficijentima iz

takav da je
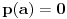
, onda se za

kaže da je transcedentan element nad poljem

i tada važi formula
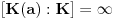
, a ako takav polinom postoji, onda kažemo da je

algebarski element nad

i važi formula da je
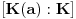
jednako najmanjem mogućem stepenu takvog polinoma.
Ako je

neko potpolje od

i

pozitivan realan broj, onda je
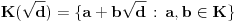
, i važi
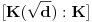
jednako 1 ako
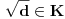
, odnosno 2 u suprotnom. U svakom slučaju je
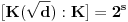
za
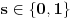
.
Dakle, ako imamo niz

potpolja od

, takvih da za sve
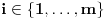
važi
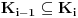
i
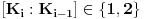
, onda je
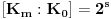
za neki ceo nenegativan broj

.
Ako je pak

potpolje od

i ako je
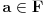
, onda je
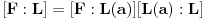
, odnosno da je
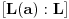
delitelj broja
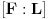
. Dakle, ako je

raširenje polja

čiji je stepen neki stepen dvojke, onda je svaki element skupa

algebarski nad

(što znači da postoji polinom sa racionalnim koeficijentima stepena barem jedan, kome je taj element jedan od korena) čiji je stepen minimalnog polinoma (takvog polinoma najmanjeg stepena) jednak nekom stepenu dvojke.
Kakve to veze ima sa geometrijskim konstrukcijama?
Neka je na početku data jedinična duž. Možemo izabrati koordinatni sistem kome je jedan od krajeva koordinatni početak, a drugi kraj duži ima koordinate

.
Osnovne konstrukcije lenjirom i šestarom su sledeće:
1. Kroz dve tačke

i

povucimo pravu

. Ako su obe koordinate tačaka

i

imale obe koordinate u nekom polju

, onda prava

ima jednačinu čiji su svi koeficijenti u polju

.
2. Konstruišimo krug

sa centrom

koji prolazi kroz tačku

. Ako tačke

i

imaju obe koordinate u polju

, onda krug

ima jednačinu koja ima sve koeficijente iz polja

.
3. Konstruišimo presečnu tačku

pravih

i

. Ako prave

i

imaju jednačine čiji svi koeficijenti leže u polju

, onda i tačka

ima obe koordinate u polju

.
4. Konstruišimo presečne tačke

i

kruga

i prave

. Ako krug

i prava

imaju jednačine čiji su svi koeficijenti u polju

, onda postoji pozitivan realan broj

takav da obe koordinate tačaka

i

pripadaju polju
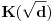
.
5. Konstruišimo presečne tačke

i

krugova


. Ako krugovi

i

imaju jednačine čiji su svi koeficijenti u polju

, onda postoji pozitivan realan broj

takav da obe koordinate tačaka

i

pripadaju polju
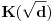
.
Pošto na početku imamo samo krajeve jedinične duži, čije su koordinate
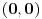
i

iz polja

, konačnom primenom navedenih osnovnih konstrukcija lenjiriom i šestarom dobijamo
a) tačke čije su obe koordinate u nekom polju

,
b) prave koje imaju jednačine sa svim koeficijentima u nekom polju

,
c) krugove koji imaju jednačine sa svim koeficijentima u nekom polju

,
pri čemu za to polje

važi da je
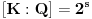
za neki ceo nenegativan broj

.
[Ovu poruku je menjao Nedeljko dana 07.08.2020. u 00:36 GMT+1]
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.