Što se samog zadatka tiče, rešenje verovatno najjednostavnije ide preko
Lebegove teoreme o gustini. Naime, iz navedene teoreme direktno sledi da postoji
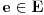
za koje je
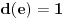
. To znači da možemo odabrati

takvo da je
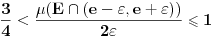
. Dokazaćemo:
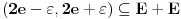
. Pretpostavimo suprotno: neka
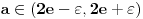
,
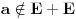
. Neka je, bez umanjenja opštosti,
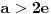
. Tada za svako
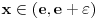
važi
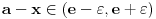
. Kako
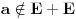
, sledi da

i

ne mogu istovremeno pripadati skupu

. Odatle su skupovi
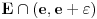
i
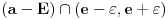
disjunktni, pa važi
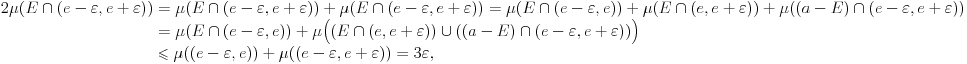
što je u kontradikciji sa izborom

.
Na isti način se dokazuje i da za dva merljiva skupa s pozitivnom Lebegovom merom,
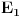
i
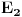
, skup
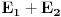
ima nepraznu unutrašnjost.
Ljubičice crvena, što si plava kô zelena trava.
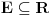 merljiv skup pozitivne Lebegove mere. Dokazati da skup
merljiv skup pozitivne Lebegove mere. Dokazati da skup 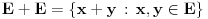 ima nepraznu unutrasnjost. Ako je nekome lakse, neka to dokaze u slucaju da je
ima nepraznu unutrasnjost. Ako je nekome lakse, neka to dokaze u slucaju da je  kompaktan skup (posto se opsti slucaj lako svodi na taj specijalan). U tom slucaju je i skup
kompaktan skup (posto se opsti slucaj lako svodi na taj specijalan). U tom slucaju je i skup 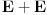 kompaktan skup.
kompaktan skup.