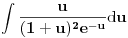Ako imaš integral oblika
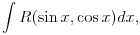
gde je
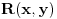
racionalna funkcija, onda možeš da koristiš smenu
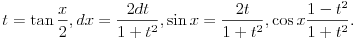
Ukoliko je pritom pointegralna funkcija neparna, onda se ona može dovesti do oblika
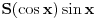
gde je

neka racionalna funkcija, pa možeš koristiti smenu
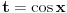
. Ukoliko je podintegralna funkcija parna, ona se može napisati kao
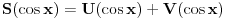
gde su
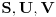
racionalne funkcije pri čemu je funkcija

parna, a funkcija

neparna. Znači, dobijamo dva integrale oblika
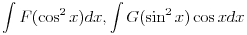
od kojih se prvi svodi na racionalnu funkciju smenom
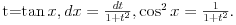
a drugi smenom
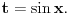
Te smene su obično zgodnije kada je podintegralna funkcija parna ili neparna. Na kraju krajeva, svaka funkcija

se može napisati kao zbir parne funkcije
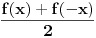
i neparne funkcije
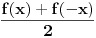
Što se tiče, integrala oblika
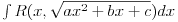
gde je

racionalna funkcija i
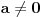
, postoje Ojlerove smene kojeih odmah prevode ove integrale u integrale racionalne funkcije. Ako je
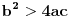
onda se može koristiti druga Ojlerova smena
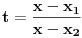
gde su
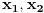
različiti koreni polinoma
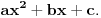
Ako je
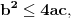
da bi integral imao smisla potkorena veličina u podintegralnoj funkciji mora da bude nenegativna na bar jednom intervalu koji se sastoji od više od jedne tačke. No, tada mora biti

pa mok\emo koristiti prvu Ojlerovu smenu
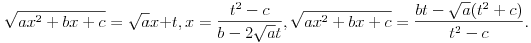
Štaviše, tada potkorena veličina mora biti nenegativna na celom skupu realnih brjeva, pa i u nuli odakle je
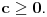
Pritom jednakost važi samo ako je
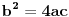
kada pod korenom imamko potpun kvadrat, pa podintegralna funkcija nije iracionalna. Dakle, zanimljiv je samo slučaj kada je
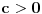
. U tom slučaju možemo koristiti treću Ojlerovu smenu
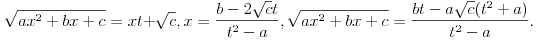
Ovi integrali se mogu svoditi i na integrale funkciaj koje se izražavaju kao racionalne funkcije trigonometrijskih ili hiperboličkih trigonometrijskih (a samim tim i preko
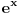
), ali ne mogu o svemu ovde da pišem. Jednostavno, ne možeš koristiti samo zbirku, već ti treba i neki udžbenik tamo svega toga već ima.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.