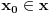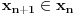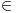Citat:
Milosh Milosavljevic1: Sustina aksiome je u tome da
nijedan skup nije element sam sebi i da
ne postoji beskonacni niz A(i) takav da je A(i+1) element A(i), za svaki prirodan broj i.
Zacrnjeno je posledica podvučenog.
Skup

je dobro zasnovan ako ne postoji niz

takav da
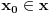
i
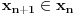
za svaki prirodan broj

. Aksioma regularnosti tvrdi da su svi skupovi takvi, tj. da nema drugih.
Dokazuje se da npr. svakoj strukturi odgovara izomorfna struktura čiji je skup nosač dobro zasnovan. Drugim rečima, ako teoriju skupova shvatimo samo kao alatku za opisivanje matematike, onda nam skupovi koji nisu dobro zasnovani nisu potrebni, a ova aksioma može biti zgodna za dokaze koji se oslanjaju na
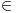
-indukciju. To je aksioma tehničkog karaktera. Teorija ZFC bez nje se smatra formalizacijom naivne teorije skupova.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.




 aksioma regularnosti
aksioma regularnosti