[es] - Paradoks u teoriji skupova

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
195.222.97.*

+2801 Profil

^{27.04.2008. u 09:58 - pre 206 meseci}

Svojevremeno sam smislio ovaj (naravno, nekorektan) dokaz da je aksioma izbora posledica ostalih aksioma teorije skupova. Zadatak je naći grešku u dokazu. Napominjem da me je mrzelo da kucam baš svaki korak, ali se sve može kompletirati i korektno sprovesti osim jedne "sitnice". Postoji samo jedna greška.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Prikačeni fajlovi

ZF_paradox.pdf - 46.29k

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.dialup.neobee.net.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+621 Profil

Re: "Paradoks" u teoriji skupova

^{06.07.2008. u 02:30 - pre 204 meseci}

Kad već niko neće, da pokušam ja.

Kažeš:

Citat:

Otuda za ma koje

iz skupa nosača

modela

postoji

takvo da u modelu

važi formula

pri valuaciji

za koju je

. Dakle, postoji funkcija

takva da za ma koje

u modelu

važi formula

pri valuaciji

za koju je

Prva rečenica konstatuje samo da su svi skupovi

neprazni. Da bi iz toga izvukao ono što tvrdiš u narednoj rečenici, moraš se pozvati na aksiomu izbora.

Doduše, formalizam mi nikad nije bio jača strana niti naročita ljubav.

_{[Ovu poruku je menjao Bojan Basic dana 06.07.2008. u 23:22 GMT+1]}

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.sbb.rs.

+2801 Profil

Re: "Paradoks" u teoriji skupova

^{07.07.2008. u 08:21 - pre 204 meseci}

Znao sam da ce neko na to da posumnja, ali taj deo uopste nije problem iz vise razloga.

1) Aksioma izbora jeste primenjena, ali na metanivou, koji se ne mesa sa objeknivoom. Dakle, ovde je ZF sistem posmatran kao formalna teorija (aksiome ZF + aksiome pred. racuna + pravila izvodjenjapred. racuna), ili preciznije teorija prvog reda. Ona nema pojma o tome na sta mi mislimo pod binarnim relacijskim znakom

. Jedino zna da ta relacija zadovoljava date aksiome, bas kao i da radimo sa nekom drugom teorijom sa jednim binarnim relacijskim znakom (npr. teorijom gustih linearnih uredjenja bez krajeva). Ovde ispitujemo da li je neki niz znakova (koji ne moras shvatiti kao aksiomu izbora) teorema jednog formalnog sistema i sasvim je svejedno da li na metanivou vazi ono sto u tvojoj glavi predstavlja tumacenje tog niza znakova. Preciznije,

Iz

sledi

, kao i

(ovo poslednje pod pretpostavkom da je ZF neprotivrecna teorija).

2) Primena aksiome izbora se moze eliminisati, jer ja sam esencijalno koristio samo teoremu o postojanju modela neprotivrecne teorije prvog reda. No, ona ima varijantu i sa najvise prebrojivim domenima, gde domen modela teorije prvog reda najvise prebrojivog jezika uvek moze biti podskup skupa prirodnih brojeva, dakle dobro uredjen skup, tako da imamo funciju izbora na njemu vec u ZF.

3) Problem koji razmatramo je konacno kombinatorne prirode (moze se kodirati u univerzumu

striktno konacnih skupova), a po teoremi apsolutnosti se sve eventualne primene AC, CH (pa i mnogo jace aksiome V=L) iz dokaza ovakvih tvrdjenja mogu eliminisati bez obzira da li smo u dokazu napustali konacno kombinatorni univerzum

ili ne.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.sbb.rs.

+2801 Profil

Re: "Paradoks" u teoriji skupova

^{07.07.2008. u 11:06 - pre 204 meseci}

Ovo pod 1) znaci da sam sredstvima teorije ZFC "dokazao" da je AC posledica ZF, to jest

. No, Pol Koen je dokazao da je

, pa bi shodno prethodnom bilo

iz cega na osnovu Gedelovih teorema nepotpunosti sledi da je ZFC teorija

-protivrecna (ili jos jace

-protivrecna). No, mada tu jos nema pravog logickog paradoksa, to znaci da teorija skupova "laze" o prirodnim brojevima, to jest, da postoje netacni iskazi o prirodnim brojevima koji su teoreme ZFC sto je "skoro paradoks".

No, ovde se radi o necem drugom. Ako bude zainteresovanih, objavicu resenje.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.dynamic.sbb.rs.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+621 Profil

Re: "Paradoks" u teoriji skupova

^{07.07.2008. u 14:17 - pre 204 meseci}

U redu, prihvatam tvoje obrazloženje dela za koji sam smatrao da je sporan. Zahvaljujem.

Ipak, voleo bih da vidim gde je zaista greška u tvom dokazu.

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu

Vincenity
student
Novi Sad

Član broj: 185662
Poruke: 12
89.216.112.*

Profil

Re: "Paradoks" u teoriji skupova

^{07.07.2008. u 16:35 - pre 204 meseci}

I ja bih bas voleo da vidim o cemu se radi...

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.sbb.rs.

+2801 Profil

Re: "Paradoks" u teoriji skupova

^{07.07.2008. u 16:38 - pre 204 meseci}

Problem je u koraku u kome se primenjuje shema zamene. Dakle, skup

je konstruisan kao

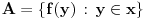
. Sta kaze shema zamene? Ako je

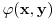
ma koja formula jezika teorije skupova, onda je formula

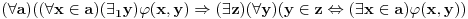
jedna instanca sheme zamene. Ovo je jedna od njenih mogucih formulacija. Slobodnije receno, ako imamo funkciju definisanu na nekom skupu formulom teorije skupova, onda postoji skup ciji su elementi tacno slike elemenata domena te funkcije.

E, pa funkcija

nije definisana formulom teorije skupova. No, to sto se koristi neki dodatni simbol koji je uveden teoremama o definicionim ekstenzijama nije uvek problem. Ako za neku formulu

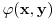
jezika

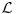
teorije

vazi

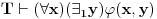
onda se novi funkcijski znak (prosirenog jezika

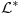
tim novim funkcijskim simbolom) uveden (novom) aksiomom

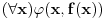
(prosirene teorije

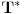
tom novom aksiomom) moze eliminisati iz svakog iskaza u smislu da za ma koju formulu

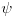
prosirenog jezika

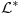
postoji formula

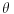
jezika

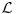
koja je njoj ekvivalentna u prosirenoj teoriji

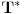
. Takodje, novouvedeni simbol se moze eliminisati iz svakog dokaza u smislu da je svaka teorema na jeziku

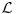
prosirene teorije

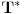
takodje teorema teorije

.

Medjutim, ako znamo samo da za formulu

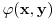
jezika

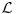
vazi

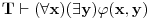
, onda za uz prethodnu simboliku mozemo zakljuciti samo da je prosirenje konzervativno za dokaze, ali ne i za iskaze. Da je aksioma izbora bila korektno dokazana u prosirenoj teoriji

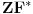
, sve bi bilo u redu. Medjutim, u dokazu je koriscena formula uljez, koja nije aksioma teorije

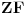
, pa cak ni ekvivalentna nekoj od aksioma, vec je samo prerusena u ruho sheme zamene. Stoga dokaz nije bio korektan ni u teoriji prosirenoj

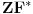
(jer je kao aksioma koriscena formula koja nije aksioma te teorije), pa se zakljucak samim tim ne moze primeniti ni na teoriju

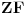
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Vincenity
student
Novi Sad

Član broj: 185662
Poruke: 12
89.216.112.*

Profil

Re: "Paradoks" u teoriji skupova

^{07.07.2008. u 16:52 - pre 204 meseci}

Ja sam prvo pomislio na shemu zamene, medjutim kada sam konsultovao literaturu nisam uspeo da vidim sta nije dobro... U sustini, problem je sto zapravo ono f nije ni funkcija, jer moze da uzima vise vrednosti za isto x? a u shemi zamene mora biti jedinstveno to sto nam treba da bi primenjivali? ili sam pogresno rastumacio...

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
79.101.186.*

+2801 Profil

Re: "Paradoks" u teoriji skupova

^{07.07.2008. u 18:06 - pre 204 meseci}

f jeste funkcijski simbol. No, u datom modelu teorije skupova ZF njegova interpretacija nije jednoznacno odredjena. Jeste funkcija, ali nije jednoznacno odredjena. Postoji vise funkcija koje mogu da zadovolje definicionu formulu u modelu teorije ZF.

Dakle, formula

je valjana formula (jer je f funkcijski znak), pa je samim tim i teorema teorije ZF.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu