[es] - jednostavan zadatak, dokazati

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
95.180.21.*

+64 Profil

^{19.06.2013. u 14:36 - pre 143 meseci}

@Nedeljko
Ocekujem od njega da prihvati argumente. A jasno je da se trudi oko svega ovoga, pa se nadam da ce se potruditi i oko razumevanja drugih...

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
95.180.21.*

+64 Profil

Re: jednostavan zadatak, dokazati

^{19.06.2013. u 14:43 - pre 143 meseci}

@number42
"za svako a, b, c koji su u obliku prve jednacine, uvek postoje neki p i q tako da je druga jednacina za svako x uvek tacna"

Vidi, ti si prvo rekao sta su a, b i c, dakle da za svaku takvu trojku vazi ono sto sledi; a ono sto sledi je da postoje p i q (dakle od tog mesta pa nadalje su i oni fiksirani), takvi da je data jednacina tacna "za svako x". To nikako ne moze. Ispada kao da mozes da izabres kakvo god x, a da sve ostalo bude isto.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.isp.telekom.rs.

+2801 Profil

Re: jednostavan zadatak, dokazati

^{19.06.2013. u 15:34 - pre 143 meseci}

Citat:

darkosos: jasno je da se trudi oko svega ovoga

Sa ovim se nikako ne slažem. U svakom slučaju se ne trudi da nauči nešto kako treba, nego... već sam napisao.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

number42

Član broj: 313623
Poruke: 426

+52 Profil

Re: jednostavan zadatak, dokazati

^{19.06.2013. u 21:07 - pre 143 meseci}

Citat:

darkosos:
ono sto sledi je da postoje p i q (dakle od tog mesta pa nadalje su i oni fiksirani)

hvala za trud na objasnjenju, ali ovo nisam napisao.

napisao sam "neki p i q", kako si i citirao u prvom delu komentara, a ne znam kakvom magijom u razumevanju postavke se to moze pretvoriti u "svaki", pa da covek skonta da su fiksirani.

bilo kako bilo, napisacu postavku simbolima sada kad budem pisao dokaz formulama, pa valjda ce biti razumljivo.

Odgovor na temu

number42

Član broj: 313623
Poruke: 426

+52 Profil

Re: jednostavan zadatak, dokazati

^{19.06.2013. u 21:35 - pre 143 meseci}

evo postavke i dokaza teoreme, valjda ce biti jasnije ovako s formulama.

1. pretpostavka

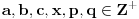
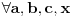
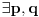
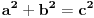
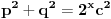
2. dokaz

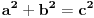
pomnozimo svaki clan sa 2

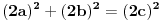
uvedemo smenu 2a=p-q i 2b=p+q

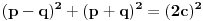
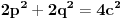
podelimo celu jednacinu sa 2

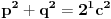
dakle dobili smo da je tacno za x=1. isti postupak je za x=3, x=5, itd.
ostaje 2 na parni stepen da bi bio ispunjen uslov "za svako x".

vracamo se na pocetak, tj jednacinu

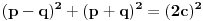
izracunamo levu stranu ali ne i desnu

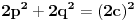
podelimo celu jednacinu sa 2

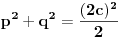
iz ovoga vidimo da se kvadrat hipotenuze (kao parnog broja) podeljen sa 2 moze uvek napisati kao zbir kvadrata.

to primenimo na sve jednacine gde je x neparno, i dobijamo da je tvrdnja tacna i za parne x, tj za svako x.

time je dokazana pocetna pretpostavka da

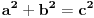
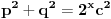
EDIT:

a ladno mi je netacan drugi deo dokaza, ovo za parne x

sad sam video.
a dobija se sasvim prosto kada se svi clanovi pomnoze sa 2 recimo, leva strana ostaje ista a desna izracuna, i dobije se 2^2, tj bilo koji parni stepen

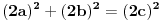
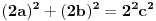_{[Ovu poruku je menjao number42 dana 20.06.2013. u 00:55 GMT+1]}

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
95.180.21.*

+64 Profil

Re: jednostavan zadatak, dokazati

^{20.06.2013. u 09:05 - pre 143 meseci}

Probacu jos jednom, a onda odustajem: napisao si:

"za svako a, b, c koji su u obliku prve jednacine, uvek postoje neki p i q tako da je druga jednacina za svako x uvek tacna".

Probacu da ispratim to sa konkretnim brojevima, da bi ti bilo jasnije:

"za svako a, b, c koji su u obliku prve jednacine"

evo izabracu 3, 4 i 5;

"uvek postoje neki p i q"

evo recimo da znam koliko su p i q (ne mogu da izaberem brojeve jer je ostatak nemoguc)

"tako da je druga jednacina za svako x uvek tacna"

Posto sam vec prema uputstvu izabrao a, b, c, p i q, jedino sto je promenljivo u "drugoj jednacini" je x. I to je naravno nemoguca situacija.

Dakle, kada sam napisao da su p i q u ostatku fiksirani, nisam mislio na:
"a ne znam kakvom magijom u razumevanju postavke se to moze pretvoriti u "svaki"";
dakle nema magije, nego logike.

Sada si napisao potpuno drugacije: stavio si "za svako x" ispred "postoje p i q" i to sada ima smisla. I sve u svemu, i pored toga sto si lose napisao na pocetku, shvatio sam sta zelis da uradis i odmah ti napisao dokaz u dva reda.

Pa sam cak pokusao da prema tvom "uputstvu" ispisem sta si radio i video da nesto nije u redu. Zato sam te zamolio da sam napises dokaz. I ispostavilo se da zaista nije u redu, jer si zamenjujuci svojom smenom napravio gresku, "ispustio" si dvojku.

I sta reci na kraju? Sam si na kraju shvatio koliko je jednostavno i da ti tvoja smena ovde nicemu ne sluzi. A ja sam ti resenje napisao u prvoj poruci. I ne znam sto se uopste mlatim sa svim ovim?

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.isp.telekom.rs.

+2801 Profil

Re: jednostavan zadatak, dokazati

^{20.06.2013. u 09:37 - pre 143 meseci}

Darko, rekao sam ti da je izlišno.

Citat:

darkosos: I ne znam sto se uopste mlatim sa svim ovim?

Upravo se o tome radi.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

number42

Član broj: 313623
Poruke: 426

+52 Profil

Re: jednostavan zadatak, dokazati

^{20.06.2013. u 10:11 - pre 143 meseci}

@darkosos,

ma ok, raspravili smo. ti mislis da je losa formulacija, ja mislim da se "neke promenjive" ne mogu transformisati tokom formulacije u "svake" ma kako da formulises, i to je to.
ova jednacina nema resenja, recimo

btw, nasao sam opsti clan. ako nam nije poznato koji su celi brojevi u pitagorinoj teoremi, desnu stranu uvek mozemo mnoziti (da bi na levoj imali neki zbir kvadrata) sa 4x^2, i 2x^2, a dokazuje se isto kao i za 2^x.

ne znam da li postoji jos neki izraz u opstem slucaju.

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
*.mts.telekom.rs.

+64 Profil

Re: jednostavan zadatak, dokazati

^{20.06.2013. u 10:18 - pre 143 meseci}

Ideja je da se usmeri energija... Naravno do neke granice. Svako ima sansu da se ispravi, dok se ne pokaze neispravljivim :) Ako moze nesto konstruktivno, moze., ako ne, bolje se izbegavati...

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
*.mts.telekom.rs.

+64 Profil

Re: jednostavan zadatak, dokazati

^{20.06.2013. u 10:29 - pre 143 meseci}

@number42
opet nisi razumeo... nisam ja nista transformisao, vec si ti stavio "za svako x" na pogresno mesto. Ovako ne ide...

Odgovor na temu

number42

Član broj: 313623
Poruke: 426

+52 Profil

Re: jednostavan zadatak, dokazati

^{20.06.2013. u 10:41 - pre 143 meseci}

@darkosos,

pa mozda si primetio, ja i izbegavam bilo kakva prepucavanja i svadje na forumu na nauci, jer mi je to prosto smesan koncept, narocito u matematici.

ne kapiram ove oblasti kao neku stvar gde se treba takmiciti, vec stvarati nove ideje, formulacije i sl, zajedno sa ljudima razlicitih senzibiliteta, nivoa znanja i kreativnosti.
sta covek ima od mehanickog razmisljanja u nauci, stvarno ne znam.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dynamic.isp.telekom.rs.

+2801 Profil

Re: jednostavan zadatak, dokazati

^{20.06.2013. u 11:40 - pre 143 meseci}

Kapiraš Darko, on neće ništa da nauči, već da "razmenjuje ideje". galet@world aka atelago je banovan. Možda mu je ovo reinkarnacija.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

darkosos
Darko Šoš
Beograd

Član broj: 5053
Poruke: 1131
95.180.21.*

+64 Profil

Re: jednostavan zadatak, dokazati

^{20.06.2013. u 12:05 - pre 143 meseci}

Ma kakogod, meni je ovo dosadilo... A valjda nema samo jedan takav :)

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: jednostavan zadatak, dokazati

^{20.06.2013. u 23:16 - pre 143 meseci}

Citat:

number42: sta covek ima od mehanickog razmisljanja u nauci, stvarno ne znam.

Samo da napomenem ostalima da se ovo odnosilo na mene.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu