Disk momenta tromosti J rotira i na njemu se radijalnom brzinom w kreće masa m.Ako su početni uslovi:
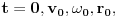
,onda je izraz za obodnu brzinu mase m:
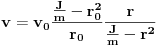
...Ova brzina ovisi o r, a izvedena je uz pomoć zakona o održanju energije.Razmotrimo najprije ekstremni slučaj.
1) Za slučaj da je moment tromosti diska zanemarivo mali (naprimjer diska uopšte nema,J=0),izraz ima oblik:
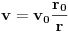
...Treba naći ubrzanje mase m.
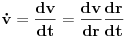
...
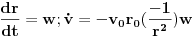
...
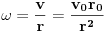
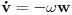
..pa je Koriolisova sila,
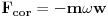
,..usporava obodnu brzinu!Kad bi w usmjerili ka centru rotacije (-w) imali bi povećanje obodne brzine.Toj sili koja mijenja obodnu brzinu opire se inercijalna sila mase m.
Evo jedan krajnje konkretan primjer:
Davidova praćka
Kažu da je ubio Golijata kamenom mase 1 kg.Dužina konopaca praćke je 0.7 m,a toliko je dugačka i ruka.Rotirajući praćku sa centrom rotacije u ramenu na radijusu r=1.4 m postigao je ugaonu brzinu od 3 obtaja u sekundi.A onda tokom zadnje rotacije privukao je šaku ka ramenu i smanjio radijus rotacije na pola.Kad je u pravom trenutku otpusto jedan konopčić kamen je izletio u pravcu Golijata.Kolika je bila brzina i energija kamena?
Najprije izračunam početne uslove:
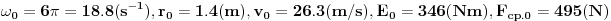
Radijalna brzina:
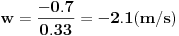
Izračunam brzinu za r=0.7(m):
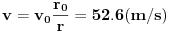
(kao kod slobodnog pada sa 140 metara visine)
Energija i centripetalna sila:
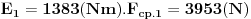
Prirast energije kamena
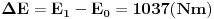
Rad centripetalne sile
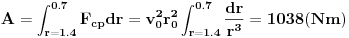
Vidi se da je prirast energije kamena jednak Davidovom radu pri savlađivanju centrifugalne sile.
Korištenjem „zvanične“ formule,
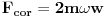
,napravili bi ogromnu grešku.Na to sam već ukazao na primjeru kod slobodnog pada.
2)(Ovdje ću u narednoj poruci razmotriti slučaj kad J nije zanemariva veličina.)
________________________________
Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500
OK evo prave formule:P=2wft^2 [period]