[es] - Da li je zakon poluge pogrešan

atelago

Član broj: 265415
Poruke: 776
*.dynamic.sbb.rs.

+53 Profil

^{24.01.2013. u 08:46 - pre 149 meseci}

Malo si se popravio, ali još si daleko:

Citat:

Nedeljko:
...ili da kretanje C nije u sistemu D,

Ne razlikuješ šta znači kretanje "u sistemu" od "kretanja u odnosu na sistem"
Kretanje "u sistemu" ne postoji već samo kretanje u odnosu na sistem

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Da li je zakon poluge pogrešan

^{24.01.2013. u 10:26 - pre 149 meseci}

Postoji samo kretanje u prostorvremenu, a to kretanje se može izraziti u bilo kom sistemu.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

atelago

Član broj: 265415
Poruke: 776
*.dynamic.sbb.rs.

+53 Profil

Re: Da li je zakon poluge pogrešan

^{24.01.2013. u 11:12 - pre 149 meseci}

Citat:

Nedeljko: Postoji samo kretanje u prostorvremenu, a to kretanje se može izraziti u bilo kom sistemu.

Postoji samo relativno kretanje i ono se može izraziti u odnosu na bilo
koji sistem koji u tom slučaju nazivamo referentni.
Kretanje je međusobna promena položaja tela. Samo tu promenu možemo konstatovati,
a ne promenu između tela i prostorvremena. Ne postoji kretanje u odnosu na prostor jer
je telo uvek u istom odnosu prema prostoru.

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2164
..able.dyn.broadband.blic.net.

+197 Profil

Re: Da li je zakon poluge pogrešan

^{24.01.2013. u 11:44 - pre 149 meseci}

@Nedeljko:"Telo se ne nalazi niukakvom sistemu, već u prostorvremenu,..."

Tako je.

@Nedeljko:"...a tačke prostorvremena se opisuju četvorkama brojeva na mnogo načina, od kojih se svaki zove koordinatni sistem."

..a tačke geometrijskog modela prostorvremena se opisuju četvorkama brojeva na mnogo načina.Veza (prevodioc) algebarskog zapisa i geometrijskog modela zove se koordinatni sistem.

@Nedeljko:"Samim tim, u svakom sistemu postoji zakon kretanja svakog tela, koji se odnosi na to telo i taj sistem."

Geometrijski model može se algebarski zapisati na različite načine korištenjem različitih koordinatnih sistema.Ovo je područje matematike i zove se kinematika.
Zbog povezanosti sa problemima u fizici uglavnom je tretiraju kao granu fizike.A neko pretjera toliko pa u to ugura silu i masu što je krajnje besmisleno.

Naprimjer veza između dva koordinatna sistema može poslužiti da se algebarski opis neke kinematičke pojave korektno prevede.Zapis napravljen pomoću jednog koosistema prevedemo u zapis drugog.Ovi zapisi nisu zakoni fizike već kinematičke jednačine (na polju s,t).

Nedopustivo je da se naprimjer drugi izvod puta po vremenu u ovakvim jednačinama pomnoži sa masom da se dobije sila.
Nedopustivo je da se veza između dva koordinetna sistema koristi za prevođenje izraza koji sadrže pojam sile.Itd..

Ovakvim radnjama se dolazi do apsurda da nam u jedačinama ne funkcionira zakon o održanju energije.Zato se moramo odlučiti:Ili odbaciti izvod izraza za Koriolisovu silu i prihvatiti zakon poluge ili oboje obratno.

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Odgovor na temu

atelago

Član broj: 265415
Poruke: 776
*.dynamic.sbb.rs.

+53 Profil

Re: Da li je zakon poluge pogrešan

^{24.01.2013. u 12:45 - pre 149 meseci}

Matematika, kinematika, inercijalni i neinercijalni sistemi su pomoće stvari koje služe
kvantitatvnoj analizi procesa u fizici.
I zato ih ne treba bagatelisati na primer na način: "Telo se ne nalazi niukakvom sistemu"
što je samo po sebi jasno, ali sistemi su uvedeni dogovorno i treba znati kakav je taj
dogovor i čemu služi.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Da li je zakon poluge pogrešan

^{24.01.2013. u 15:41 - pre 149 meseci}

Citat:

zzzz: Ovakvim radnjama se dolazi do apsurda da nam u jedačinama ne funkcionira zakon o održanju energije.

Dokaži.

Na celoj ovoj temi pokušavaš da dokažeš da zakon poluge važi u klasičnoj mehanici i da ima potporu u eksperimentima u okolnostima u kojima se klasična mehanika primenjuje. Dobro jutro Kolumbo! Onda ispituješ na analogan način Kuriolisovu silu, koja je specijalan slučaj inercijalne. To je sve raspravljeno odavno i ne vidim svrhu takvih rasprava.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2164
..able.dyn.broadband.blic.net.

+197 Profil

Re: Da li je zakon poluge pogrešan

^{25.01.2013. u 00:51 - pre 149 meseci}

Citat:

Nedeljko: Dokaži.

Na celoj ovoj temi pokušavaš da dokažeš da zakon poluge važi u klasičnoj mehanici i da ima potporu u eksperimentima u okolnostima u kojima se klasična mehanika primenjuje. Dobro jutro Kolumbo! Onda ispituješ na analogan način Kuriolisovu silu, koja je specijalan slučaj inercijalne. To je sve raspravljeno odavno i ne vidim svrhu takvih rasprava.

Čak i u najdogmatskijim religijama ponekad se ukaže potreba da se nešto preispita.Naprimjer Papa rimski sazove koncil iako je ta religija definisana prije nekih 2000 godina.Zašto se ti Nedeljko osjećaš tako jadno inferiorno i ne usuđuješ kritički razmotriti nešto što je uvedeno u nauku prije 180 godina.A taj ko je to uveo (siguran sam) nije imao toliko jako školsko obrazovanje kao ti.

Nisam ja bezveze pokrenuo ovu temu.Postoji konfuzija u literaturi po pitanju definicije Koriolisove sile.Naveo sam ja te primjere,činimi se bar 3.Oprečni su ta sveučilišna tumačenja.Zar nisi primjetio.
Tu vlada haos u tumačenju.Stičem utisak da mnogi pisci skripata nemaju pojma o tome.A šta tek znaju studenti koji polože ispit iz takvih skripti.Ništa,a šta će im takve gluposti?Jel tako?

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Odgovor na temu

atelago

Član broj: 265415
Poruke: 776
*.dynamic.sbb.rs.

+53 Profil

Re: Da li je zakon poluge pogrešan

^{25.01.2013. u 07:28 - pre 149 meseci}

"Jako školsko obrazovanje" stečeno bez razumevanja nema nikakvu vrednost
u pogledu suštinskog preispitivanja problematičnih zaključaka.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Da li je zakon poluge pogrešan

^{25.01.2013. u 08:44 - pre 149 meseci}

Pa, znaš šta, da danas ima nečega nepoznatog u osnovama Njutnove mehanike ili da manjka eksperimentalna podrška, ne bi se u CERN-u bavili Higsovim bozonom, nego time. Zar nisi primetio da se niko ozviljan ne bavi osnovama klasične mehanike? Klasična mehanika se izučava i dan-danas, ali se maklo dalje od osnova.

A za poređenje nečega toliko eksperimentalno isproveravanog sa religijama nemam reči.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

atelago

Član broj: 265415
Poruke: 776
*.dynamic.sbb.rs.

+53 Profil

Re: Da li je zakon poluge pogrešan

^{25.01.2013. u 14:47 - pre 149 meseci}

1. Ako pretpostavimo da zarotirani disk konstantnom ugaonom brzinom ima vrlo
veliku masu u odnosu na pokretnu masu onda preraspodelu energije između
diska i pokretne mase možemo zanemariti.

2. Ako pretpostavimo da pokretna masa ima konstantu brzinu po žlebu na disku
koji je postavljen radijalno od centra prema obodu, onda pokretna masa ima
tangencijalno ubrzanje u odnosu na disk jer prelazi sve veće puteve u jedinici
vremena u tangencijalnom smeru na disk. To ubrzanje je konstantno.

3. Ako na pokretnu masu deluje konstantna sila u smeru od centra diska prema
obodu onda masa ima konstantno ubrzanje u radijalnom smeru pa je ukupno
ubrzanje jednako vektorskom zbiru ovog ubrzanja i prethodnog.

4. Ako se pokretna masa kreće radijalno pod dejstvom centrifugalne sile onda je
telo pod dejstvom promenljive sile jer je skalarna vrednost centrifugalna sile
proporcionalna udaljenosti od centra diska. U tom slučaju pokretno telo se ne
kreće pod dejstvom konstantne sile pa ni ubrzanje nije konstantno nego se to
ubrzanje menja – postoji, dakle, prirast ubrzanja odnosno ubrzanje ubrzanja.

5. Ako pretpostavimo realan odnos masa diska i pokretne mase gde dolazi do
preraspodele energije, onda već pod 2. nemamo konstantno ubrzanje jer su
tangencijalne brzine diska i tangencijalna brzina pokretne mase promenljive,
a to posle utiče na složenost tačaka 3 i 4.

Sve u svemu, čini mi se da je sračunavanje Koriolisove sile i ubrzanja u opštem
slučaju vrlo složen problem.

Ja ne znam da li je ovaj problem ovako formulisan uopšte negde rešen, pa ni
primedbe kojekakvih pametnjakovića ne treba uzimati u obzir ako te vrdalame
ne kažu ništa konkretno o problemu ili o njegovom rešenju.

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2164
..able.dyn.broadband.blic.net.

+197 Profil

Re: Da li je zakon poluge pogrešan

^{26.01.2013. u 11:59 - pre 149 meseci}

Citat:

atelago:

Sve u svemu, čini mi se da je sračunavanje Koriolisove sile i ubrzanja u opštem
slučaju vrlo složen problem.

Ja ne znam da li je ovaj problem ovako formulisan uopšte negde rešen, pa ni
primedbe kojekakvih pametnjakovića ne treba uzimati u obzir ako te vrdalame
ne kažu ništa konkretno o problemu ili o njegovom rešenju.

Nije baš pretjerano teško napraviti taj račun.Uradiću to čim prije.Nisam dosad naišao čak ni na pokušaj rješavanja.

Nedavno sam pisao da u literaturi imamo tešku konfuziju po načinu definisanja i izvođenja Koriolisove sile.Obično ako nekog citiram ovdje,u skladu sa željom za pristojnim ponašanjem,obavjestim autora.Naprimjer za:
http://www.scribd.com/doc/38857874/skripta-OF1-1
prof Emil Babić (Opća fizika 1,na prvoj godini istraživačkog smjera studija fizike.)
(Moj dopis)

Citat:

Štovani,

Želim Vas obavjestiti da sam na jednom forumu koristio citat iz skripta
prof.Emila Babića.Ne bih želio da me krivo shvatite,jer mi ni u kom
slučaju nije bila namjera da omalovažim cjenjenog profesora.Naprotiv bio
bih zahvalan ako to pogledate na- http://www.elitesecurity.org/p3229064, i
date svoj komentar.Ako pak želite da se to obriše,uradiću tako.

Pozdrav,

Milan Kecman

Nisam dobio direktan odgovor,žao mi je.Ali indirektan jesam.Tog poglavlja sada nema u navedenoj skripti.Ko je prije otvarao taj link neka sada provjeri.Izgleda da Nedeljko nije u pravu kad tvrdi da je to sve milion puta prežvakano.Treba još žvakanja izgleda.

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Da li je zakon poluge pogrešan

^{26.01.2013. u 15:34 - pre 149 meseci}

Citat:

zzzz: Izgleda da Nedeljko nije u pravu kad tvrdi da je to sve milion puta prežvakano. Treba još žvakanja izgleda.

Pa, ništa, ti onda objavi naučni rad o tome šta je nepoznato i novim saznanjima. Ako nijedan časopis sa recenzijom ne bude hteo da štampa, onda izbacivanje nekog poglavlja iz neke knjige/skripte znači samo da je iz te knjige/skripte izbačeno to poglavlje, a ne i da se radi o nečemu nepoznatom u nauci.

_{[Ovu poruku je menjao Nedeljko dana 26.01.2013. u 17:10 GMT+1]}

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

bigkandor
Antispin Technologies

Član broj: 300656
Poruke: 252
*.yourproxyhost.com.

+228 Profil

Re: Da li je zakon poluge pogrešan

^{26.01.2013. u 16:38 - pre 149 meseci}

Citat:

zzzz: Izgleda da Nedeljko nije u pravu kad tvrdi da je to sve milion puta prežvakano. Treba još žvakanja izgleda.

Pa ako si siguran da si u pravu trebalo bi da objaviš rad. Možda nešto profitiraš. Sumnjam da će neko na ovom forumu detaljno proveravati to što računaš. Možda Nedeljko ako ga isprovociraš. Ipak, potrebna ti je i neka eksperimentalna potvrda.

Pri tome imaj na umu da tvoje izvodjenje mora biti u skladu sa danas poznatim činjenicama. Na primer, probaj da objasniš odstupanja u vibraciono-rotacionim spektrima poliatomskih molekula a koja se objašnjavaju upravo uticajem Korilisove sile.

Odgovor na temu

zzzz
milan kecman
bluka

Član broj: 11810
Poruke: 2164
..able.dyn.broadband.blic.net.

+197 Profil

Re: Da li je zakon poluge pogrešan

^{27.01.2013. u 16:32 - pre 149 meseci}

Navešću još jedan primjer krivog tumačenja Koriolisove sile.Pogledajmo ovu skriptu: http://www.fer.unizg.hr/_download/repository/predavanja9-2012.pdf
Na četvrtoj strani je izvedeno tangencijalno ubrzanje.Citat
“Tangencijalna akceleracija nastaje i zbog promjene radijalne brzine tijela po smjeru i
zbog promjene tangencijalne komponente brzine po iznosu:..“
Na petoj strani je na osnovu prethodnog izvedena Koriolisova sila.
Na šestoj je prikazan uticaj te sile pri slobodnom padu.Izračunato je koliko će biti bočno pomjeranje
zbog djelovanja Koriolisovog ubrzanja.(Ja ću to ovdje prikazati kao da je na ekvatoru)

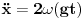
.Iintegracijom dobijemo horizontalnu brzinu,

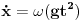
,zatim i put,

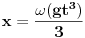
Ovo je očigledno pogrešno.Trebalo je računati samo sa ubrzanjem zbog promjene smjera.

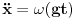
..Masa m pri padu nije ničim prisiljavana da ide vertikalno.A upravom iz tog uvjeta nastaje promjena obodne brzine i odatle je izvedena druga polovina Koriolisovog ubrzanja.
To je dobar razlog da se redefiniše Koriolisovo ubrzanje i u obzir uzme samo promjena brzine po smjeru (zbog rotacije).

Dokazati da je račun pogrešan je posve jednostavno pod uslovom da vjerujemo u ispravnost zakona o očuvanju energije.Evo dokaza:
Neka tijelo pada sa visine H.Pronađimo vrijeme padanja.

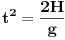
,uvrstimo u jednačinu za brzinu

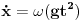
pa dobijemo:

,
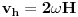
Znamo da je razlika obodnih brzina između one na visini H i na Zemlji:

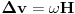
Moramo se upitati otkud nasta ta dodatna energija jer se horizontalna komponenta brzine tokom pada povećala.

_{[Ovu poruku je menjao zzzz dana 27.01.2013. u 18:09 GMT+1]}

________________________________

Najbolja kritika formule za Sagnac effect:
https://www.omicsonline.org/op...090-0902-1000189.php?aid=78500

OK evo prave formule:P=2wft^2 [period]

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Da li je zakon poluge pogrešan

^{28.01.2013. u 09:28 - pre 149 meseci}

I šta bi na kraju, je li zakon poluge važi ili je cela fizika samo nečija obična sprdnja?

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

atelago

Član broj: 265415
Poruke: 776
*.dynamic.sbb.rs.

+53 Profil

Re: Da li je zakon poluge pogrešan

^{28.01.2013. u 12:05 - pre 149 meseci}

Naravno da važi, ali ne važi sprdnja od teorije koja ga negira.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Da li je zakon poluge pogrešan

^{28.01.2013. u 12:08 - pre 149 meseci}

Slažem se. Pritom to svakako nije neka od teorija koju ne znate, već koju ste vi izmislili.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

atelago

Član broj: 265415
Poruke: 776
*.dynamic.sbb.rs.

+53 Profil

Re: Da li je zakon poluge pogrešan

^{28.01.2013. u 14:14 - pre 149 meseci}

Citat:

Nedeljko: Slažem se.

S lažeš se!

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Da li je zakon poluge pogrešan

^{28.01.2013. u 15:21 - pre 149 meseci}

Slažem se sa oonim što si napisao. Postavlja se samo pitanje kako se zove ta sprdnja od teorije koja negira princip poluge? Da nije možda "kako mali Perica zamišlja teoriju relativnosti"?

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu