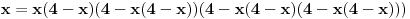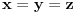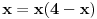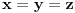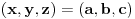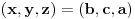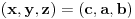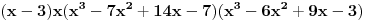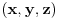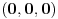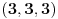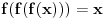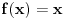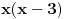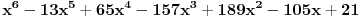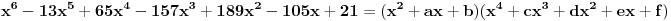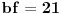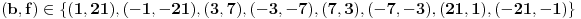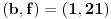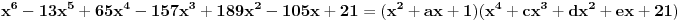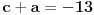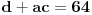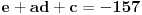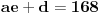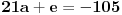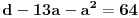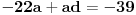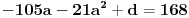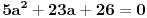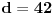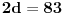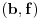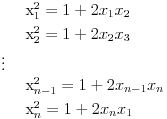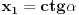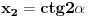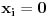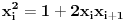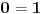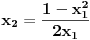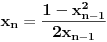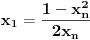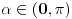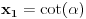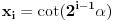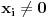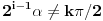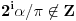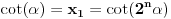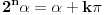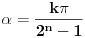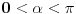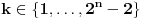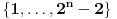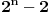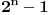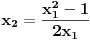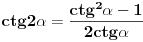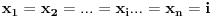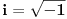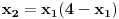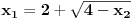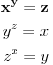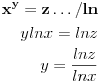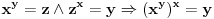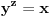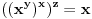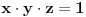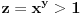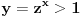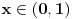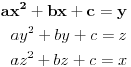Nađeš racionalne nule, pa podeliš polinom sa
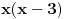
. Ostaće ti polinom
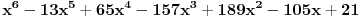
Najpre, po Gausovoj lemi je polinom sa celobrojnim koeficijentima rastavljiva nad poljem racionalnih brojeva akko je rastavljiv nad prstenom celih brojeva. Dakle, tražimo celobrojna rastavljanja. Prvo se konstatuje da nema linearnih činioca jer nema rcaionalnih korena. Pretpostavimo da ima činilaca stepena dva sa celim koeficijentima, tj. da se može napisati kao proizvod polinoma stepena dva i četiri sa celim koeficijentima. Bez umanjenja opštosti možemo pretpostaviti da je vodeći koeficijent činioca stepena dva pozitivan. Samim tim, takav mora biti i vodeći koeficijent činioca stepena četiri. No, pošto je njihov proizvod jednak 1, onda svaki od njih mora biti 1.
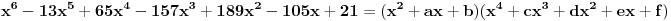
.
Prvo,
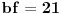
, pa
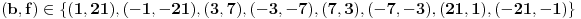
.
Ako je npr.
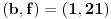
, onda jednakost
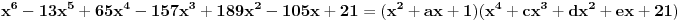
postaje sistem
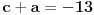
,
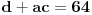
,
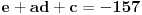
,
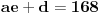
,
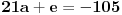
.
Dakle, imaš pet jednačina sa četiri nepoznate, pa petljaj s njima malo dok ne dobiješ kontradikciju. Recimo iz prve jednačine možeš da eliminišeš c, a iz pete e.
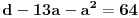
,
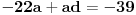
,
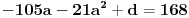
.
Oduzimanjem prve jednačine od treće dobija se da je
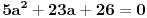
,
čije je celobrojno rešenje -2. Zamenom dobijamo da je
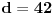
,
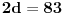
,
što je očigledna kontradikcija.
Tako se odbaci jedan po jean od parova kandidata za
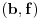
i konstatuje da nema činilaca sa celim koeficijentima stepena 2. Na sličan način se radi i sa činiocima stepena 3, s tim da, pošto su istog stepena, možemo pretpostaviti da je apsolutna vrednost slobodnog člana prvog činioca veća ili jednaka apsolutnoj vrednosti drugog činioca, pa imamo četiri slučaja umesto osam. Naravno, čim pogodimo jedan činilac, završili smo posao. Nema potrebe razmatrati i ostale slučajeve.
Lično ne smatram da je ovakav zadatak primereno dati kao jedan od četiri zadatka na ispitu koji traje četiri sata. No, to je na onima koji zadaju zadatke da odmere vreme potrebno za njihovu izradu.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
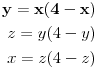




 Ciklicni sistem jednacina
Ciklicni sistem jednacina