Za
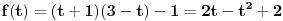
je
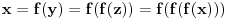
. Dakle,
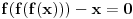
. Faktorizacijom ove jednačine dobijamo da je
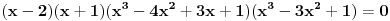
.
Dakle,

može biti

ili

ili koren jednog od navedena dva kubna polinoma. Ako je
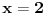
ili
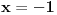
, onda je svakako
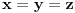
.
Sa druge strane, ako je
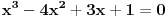
, onda su i

i

koreni istog tog polinoma i to međusobno različiti, jer kada bi na primer bilo

, onda bi zbog
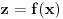
ta vrednost bila nepokretna tačka funkcije

, a to su samo

i

, što nisu koreni tog polinoma trećeg stepena.
Isto važi i u slučaju
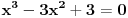
važi analogno.
Dakle, ili je
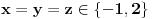
ili su
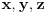
koreni istog od navedena dva kubna polinoma, ne u bilo kojoj permutaciji, nego u tri od šest mogućih permutacija, odnosno, ne mora biti
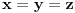
.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
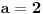 ,
, 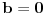 i
i 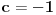 jedno od rešenja je
jedno od rešenja je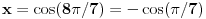 ,
, 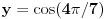 ,
, 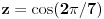 .
.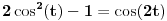 lako je proveriti da je to zaista rešenje.
lako je proveriti da je to zaista rešenje.