[es] - Diskusija resivost integralne jednacine

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.uns.ac.rs.

+33 Profil

Diskusija resivost integralne jednacine

^{26.12.2011. u 10:55 - pre 162 meseci}

Uz ovu poruku prikacicu ono sto je ranije bilo okaceno na forumu isecak iz knjige Diferencijalne jednacine 2 koji obradjuje Integralne jednacine. Mene zanima Fredholmova jednacina sa degenerisanim jezgrom. Strana 178. pa nadalje. Moj problem je sto se dobije sistem linearnih jednacina iz pretpostavke da jednacina ima resenje da bi se zatim iz sistema diskutovalo ima li jednacina ili nema resenje. Meni to lici na tesku muljavinu. Mi diskutujemo sistem (5.29) i na osnovu toga da li jna ima ili nema resenje. A do tog sistema smo dosli eksplicitno pretpostavljajuci da jednacina ima resenje. Ima li neko razumno objasnjenje za ovo?

Iz meni nepoznatog razloga ne mogu da uploadujem fajl. Profesorka Knezevic Diferencijalne jednacine 2. Rekao sam ipak gde je problem, pa ako neko moze da mi da neki odgovor bio bih mu zahvalan.

_{[Ovu poruku je menjao petarm dana 26.12.2011. u 12:07 GMT+1]}

http://www.svijetfizike.com/

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Diskusija resivost integralne jednacine

^{26.12.2011. u 11:41 - pre 162 meseci}

Fajl neće da ti se pošalje ako je veći od jednog megabajta. Ako si skenirao list u previsokoj rezoluciji, moraćeš da pretvoriš u sliku niže rezolucije, po mogućstvu u kpg formatu.

Pitanje mi nije baš najjasnije, pa da ne bih širio celu priču, okači taj list ili prekucaj relevantan deo.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.uns.ac.rs.

+33 Profil

Re: Diskusija resivost integralne jednacine

^{26.12.2011. u 12:29 - pre 162 meseci}

Evo integralne jednacine

Ovu jednacinu mozemo napisati u obliku

Ovi integrali

su konstante.

Pa jednacina postaje

Pa se resavanje integralne jednacine svodi na odredjivanje konstanti

U knjizi koju sam pomenuo kaze pretpostavimo da

zadovoljava integralnu jednacinu, pa imamo

Kako su u poslednja dva izraza leve strane jednake, jednake su i desne. I odatle obzirom da je

razlicito od nule i da su

linearno nezavisni dobijamo sistem jednacina

gde je

I u knjizi pisi ako je ovaj sistem resiv resiva je i polazna integralna jednacina. I sad mi ispitujemo resivost sistema. Ono sto je meni problem u celoj prici je da smo mi dosli do ovog sistema pretpostavljajuci da jednacina ima resenje. Inace ovaj sistem ne bismo ni dobili.

http://www.svijetfizike.com/

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Diskusija resivost integralne jednacine

^{26.12.2011. u 13:10 - pre 162 meseci}

Ako iz postojanja rešenja poslednjeg sistema sledi da ima rešenja, onda ako ga nema, moraš usput dobiti kontradikciju (nema gde) ili krajnji sistem koji nema rešenja. Iz pretpostavke da rešenje postoji dobijaš kontradikciju, odakle zaključuješ da nema rešenja. Ako rešenje postoji, ti si radio sa proizvoljnom rešenjem, pa ćeš dobiti opšte rešenje. Da li je sada jasnije?

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.uns.ac.rs.

+33 Profil

Re: Diskusija resivost integralne jednacine

^{26.12.2011. u 13:30 - pre 162 meseci}

Ja definisem determinantu sistema

za koje je

razlicito od nule sistem ima resenje. Za neke

i u tom slucaju sistem nema resenja. To je zakljucak. Mene ovo buni. Ovde se ne spominje nikakva kontradikcija u knjizi. Buni me jos jednom to sto oba ova slucaja odgovaraju integralnoj jednacini za koju smo pretpostavili da ima resenja. Mozes li dati malo vise detalja.

http://www.svijetfizike.com/

Prikačeni fajlovi

Integralne_jednacine-page-018.jpg - 230.62k

Integralne_jednacine-page-019.jpg - 217.57k

Integralne_jednacine-page-020.jpg - 252.79k

Odgovor na temu

petarm
Petar Mali
Zrenjanin

Član broj: 20220
Poruke: 1879
*.uns.ac.rs.

+33 Profil

Re: Diskusija resivost integralne jednacine

^{26.12.2011. u 13:57 - pre 162 meseci}

Prikacio sam 3 strane koje su bitne.

http://www.svijetfizike.com/

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.3gnet.mts.telekom.rs.

+2801 Profil

Re: Diskusija resivost integralne jednacine

^{26.12.2011. u 14:50 - pre 162 meseci}

Opšti pristup u matematici je sledeći: Kada rešavaš neki sistem uslova, obično iz njega izvlačiš razne zaključke (posledice) radeći sa proizvoljnim pretpostavljenim rešenjem dok ne dođeš do nekog oblika koji smatraš rešenim. Time dokazuješ formulu oblika

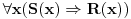
, gde je

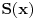
polazni sistem uslova, a

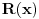
sistem uslova u rešenom obliku. Time si siguran da si obuhvatio sva eventualna rešenja, ali su se možda provukla još neka tzv. nerešenja. Onda pođeš od tog rešenog oblika ne bili proverio da li zaista zadovoljava polazni sistem uslova. Ona rešenja koja zadovolje polazni sistem uslova su tačno sva njegova rešenja.

Pretpostavimo da dati sistem linearnih jednačina ima rešenje i izaberimo jedno od njih. Ono nam daje neku funkciju

(1)

.

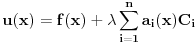
Treba proveriti da li ta funkcija zadovoljava polaznu jednačinu.

Pre svega,

.

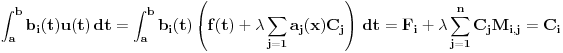
Otuda se zamenom ovako izabrane funkcije

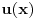
u polaznoj jednačini dobija jednačina (1), pa pošto je jednačina (1) tačna na osnovu izbora funkcije

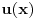
, zadovoljena je i polazna jednačina, pa ona stvarno ima rešenja.

Stoga rešavanjem ovog sistema linearnih jednačina zaista dobijaš tačno sva rešenja polazne integralne jednačine.

_{[Ovu poruku je menjao Nedeljko dana 26.12.2011. u 16:12 GMT+1]}

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu