Znaš kako, jednačine trećeg i četvrtog stepena se mogu rešiti preko korenih funkcija, ali ti se na pismenom to najverovatnije ne traži na pismenom.
Prvo jednačinu
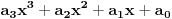
,
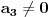
podeli sa
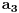
da bi dobila ekvivalentnu jednačinu sa vodećim koeficijentom jednakim 1, tj. oblika
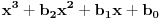
. Onda uvedi smenu
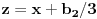
. Dobićeš jednačinu oblika
(1)
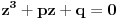
,
tj. koeficijent uz
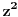
će biti 0. Slučaj kada je
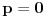
je trivijalan. Razmotrimo zato slučaj
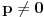
.
Sada zameni

sa
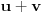
.
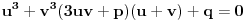
.
Uz uslov
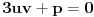
ova jednačina se svodi na
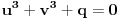
.
Dakle, treba rešiti sistem
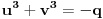
,
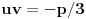
.
Jasno je da svako rešenje ovog sistema daje po jedno rešenje jednačine (1), a obzirom da za ma koje
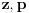
postoje
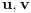
takvi da je
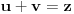
i
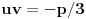
, time su obuhvaćena sva rešenja.
Dakle,
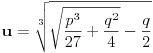
,
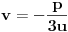
,
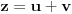
.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.