Citat:
Moze formula ili algoritam kako se dolazi do formule koji je
prilagodljiv primeni na racunaru.
Pa, na primer:
Zakači po vektor za težišta oba trougla, tako da je svaki normalan na odgovarajuću ravan. Vodi računa o orijentaciji vektora, npr tako što ako je težište T napraviš normalu kao
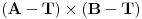
. Primeti da je treća tačka implicitno sadržana u T.
- Nađi rotaciju koja čini da ta dva vektora daju maksimalan skalarni
proizvod. (ne bi smelo da bude problem, jer je u pitanju osnovna
analitička geometriija) To je rotacija sa osom normalnom na ravan koju čine dotična dva vektora.
- Nađi rotaciju koja među-sliku preslikava tako da polazni vektori
ostanu paralelni, a da vektori od težišta do odgovarajućih temena
postanu kolinearni. To je rotacija sa osom paralelnom vektorima težišta, a koja prolazi kroz koordinatni početak.
- Kompozicija ove dve rotacije ti je rotacija koju tražiš.
- Transliraj novu među-sliku tako da se koordinate težišta poklope. To
je komponenta translacije koju tražiš.
- Na tačku D primeni, ovim redom, nađene translacije i rotacije.
Ovako dobijena transformacija bi trebalo da ispunjava uslove koje si
postavio.
f
transformacije u prostoru
