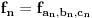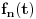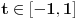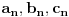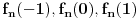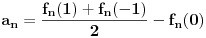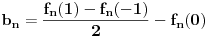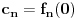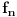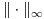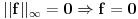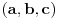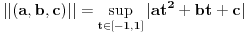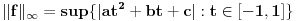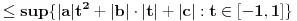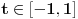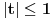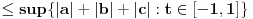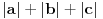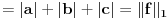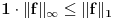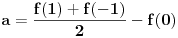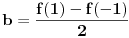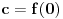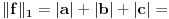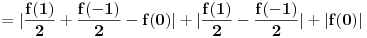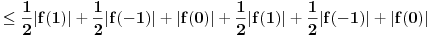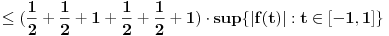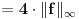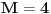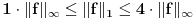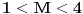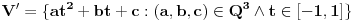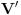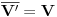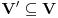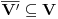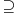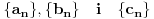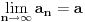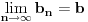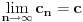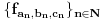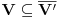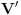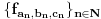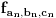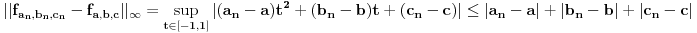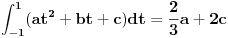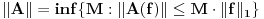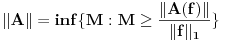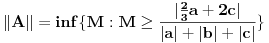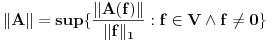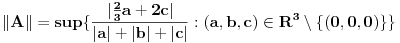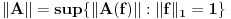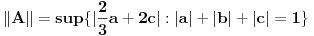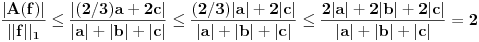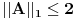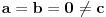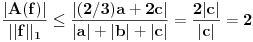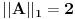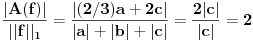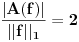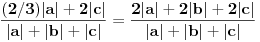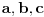Zadatak iz funkcionalne analize
, sa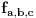 
, označimo preslikavanje intervala 
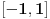u skup 
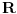dato sa: 
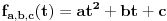za sve 
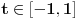. Neka je 
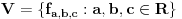.Dokazati:
a) Ako je sabiranje funkcija i množenje funkcije skalarom definisano na uobičajen način, onda je
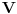vektorski prostor nad 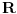, i sa 
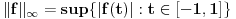je definisana norma nad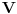 b) Sa
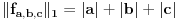je definisana još jedna norma na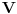 c)
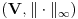je Banahov prostor.d)
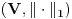je Banahov prostore) Postoje realni pozitivni brojevi
i 
, takvi da za svako 
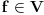važi: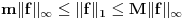 
f) V je konačno-dimenzionalan vektorski prostor. Odrediti dimenziju V i naći jednu bazu.
g)
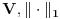je separabilan prostor.h) Neka je na V norma
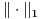. Preslikavanje 
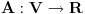dato sa: 
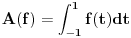je linearno i neprekidno. Odrediti mu normu.E, ovo je bio zadatak. Stavke pod a) i b) su prilično dugačke, ali prilično jasne, a ja sam se zakucao kod c). Potrebno je da dokažem da prizvoljan Košijev niz u V konvergira. Ideja mi je da ako uzmem neki Košijev niz funkcija u V
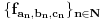gde su 
, 
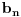i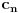 
realni brojni nizovi, dokažem da su svi ovi nizovi Košijevi, pa da su, pošto su u 
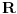, konvergentni, pa da na osnovu toga dokažem da je i niz 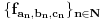konvergentan. Problem je, međutim, što mi već tri sata uspeva da dokažem da je Košijev samo 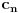, a za i 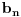nikako ne mogu da dokažem.Da ne dužim mnogo bio bih jako zahvalan kada bi mi neko dao makar smernicu kako da to dokažem, ili, eventualno, kada bi neko rekao da je put kojim sam krenuo pogrešan. Btw, ovo mi je bitno jer imam osećaj da je ovo pod c) ključno za rešavanje ostatka ovog zadatka.
PS. Dokazao sam d) i f) a ostale još nisam ni pokušavao.
