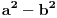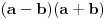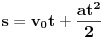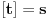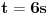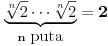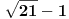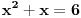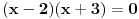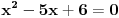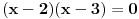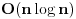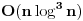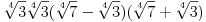 (nisam nigdje spomenuo proste faktre, nego prosto rjesenje) mislim da znas o cemu ja pricam. kad dobijes neko rjesenje koje, da tako kazem, "nije fino" onda se zapitas da li je ono i tacno. obicno se rjesenja stimaju da budu fina, okrugli brojevi itd itd... s ovom temom sam zavrsio, posto dalja rasprava nece pomoci nikome.
(nisam nigdje spomenuo proste faktre, nego prosto rjesenje) mislim da znas o cemu ja pricam. kad dobijes neko rjesenje koje, da tako kazem, "nije fino" onda se zapitas da li je ono i tacno. obicno se rjesenja stimaju da budu fina, okrugli brojevi itd itd... s ovom temom sam zavrsio, posto dalja rasprava nece pomoci nikome.A zašto je
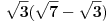 prostije od
prostije od 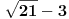 ?
?mora prići sa najjednostavnijim zadacima.
Naprimjer:
-Razlika kvadrata a^2+b^2=(a-b)(a+b)
1)Insistirati da se to zapamti napamet.
2)Nacrtati geometrijsku slikicu, od većeg kvadrata isjeći manji, pa pokazati
da se može napraviti pravougaonik od tog ostatka.Dati priliku da dijete skuži
kolike su stranice tog pravougaonika, i poveže to sa zapamćenom jednačinom.
3)Naučiti dijete da množi (a+b) sa (a-b).
4)Zadati da samostalno riješi nešto ovako: M^2-N^2=? i slični zadaci.
Ovo je dovoljno posla za jedan dan, s tim da sve treba ponoviti bar na kratko
u narednih nekoliko dana.
Ovo je skroz OK, ali nema veze sa onim o čemu pričamo.
Najteži su oni zadaci kod kojih treba gledati u pasulj šta neko od tebe očekuje.
Imao sam na fakultetu problema na ispitu sa jednim takvim nedorečenim asistentom.
Zada zadatak iz parcijalnih jednačina koji se lako rešava primenom kompleksne analize, a onda kaže "Nemojte koristiti KA, osim nešto malo, elementarno.". I onda sam ja trebao da pogađam šta je on zamislio, jer nije hteo da kaže. Pitao sam, može li ovo, može li ono, trt mrt, da bi se na kraju ispostavilo da se smeju koristiti Koši-Rimanovi uslovi. Pre toga je na ispitu iz DJ zadao zadatak za koje prirodne brojeve
 postoji diferencijalna jednačina oblika
postoji diferencijalna jednačina oblika 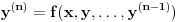 takva da važi neki uslov vezan za rešenja. Nije hteo da kaže kojoj klasi funkcija treba da pripada funkcija
takva da važi neki uslov vezan za rešenja. Nije hteo da kaže kojoj klasi funkcija treba da pripada funkcija  , a rešenje je bitno zavisilo od toga da li je to klasa neprekidnih ili Lipšicovih funkcija. Posle ispita se ispostavilo da je mislio na Lipšicove.
, a rešenje je bitno zavisilo od toga da li je to klasa neprekidnih ili Lipšicovih funkcija. Posle ispita se ispostavilo da je mislio na Lipšicove.Ovakvim pristupom đaci mogu samo da nauče da je nešto "ono što nastavnik radi onako" i onda se čudimo zašto matematiku ne razumeju i na kraju ne umeju da je primene u praksi, jer se matematika predaje na način na koji se ne može razumeti. PISA testovi sve pokazuju.




 Re: Rastavljanje polinoma na faktore-treba mi pomoc
Re: Rastavljanje polinoma na faktore-treba mi pomoc