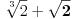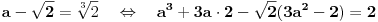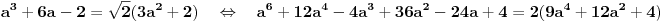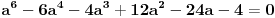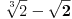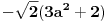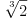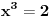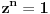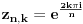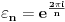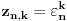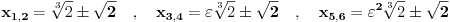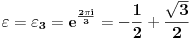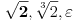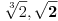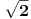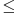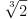Hajde da prvo nađemo polinom kojeg će poništiti naš broj a=
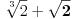
. Tada važi
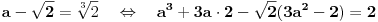
tj
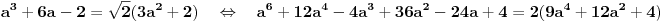
odnosno
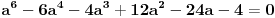
Da smo posmatrali
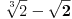
, sa desne strane bi smo dobili
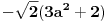
, no posle kvadriranja minus bi se izgubio, te bi smo dobili isti polinom.
Da li bi smo umesto
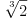
mogli da stavimo neki drugi broj, koji bi posle kubiranja opet dao dva? Koja
su rešenja jednačine
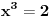
Na kraju se svede na jednačine tipa
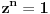
. Njihova rešenja su brojevi
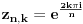
Obeležimo sa
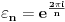
. Tada je
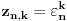
.
Rešenja naše jednačine su
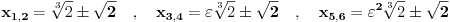
Gde je
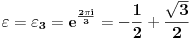
Korensko polje K=Q[

]=Q[
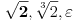
].
Prethodnu tvrdnju treba dokazati, a to me mrzi.(Nisam na ispitu). Potreban & dovoljan uslov je da
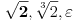
pripadaju korenskom polju, i da rešenja jednačine pripadaju ovom drugom polju.
Za kraj |K:Q|=|K:L1||L1:L2||L2:Q| gde je L1=Q[
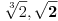
], L2=Q[
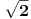
], te samim tim
|K:Q|=12
Pri tom treba dokazati da
|L2:Q|=2 (trivijalno)
L1 je potpolje od K (trivijalno)
|K:L1|>1 (jer K ima complex brojeve u sebi, L1 nema),
|K:L1|
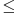
2 (postoji polinom drugog stepena iz L1[x] koji poništava

) (isto trivijalno)
L2 je potpolje L1 (trivijalno)
|L1:L2|
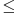
3 (postoji polinom trećeg stepena iz L2[x] koji poništava
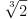
)(opet trivijalno)
|L1:L2|>2 (ne postoji polinom drugog stepena iz L2[x] koji poništava
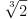
)(Naporno)
Kao što se može videti ČISTI ŠABLON.
PS Znam da je prošlo mnoooogo vremena, ali možda ipak posluži.
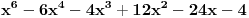
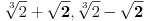 i neke cetiri kompleksne, ne znam koje)
i neke cetiri kompleksne, ne znam koje)



 Korensko polje - ko zna algebru?
Korensko polje - ko zna algebru?