Zadatak:
Nazovimo
kukom figuru sastavljenu od 6 jediničnih kvadrata kao na slici.
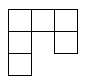
Odrediti sve
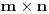
pravougaonike koji se mogu pokriti kukama. Pravougaonik pokrivamo bez preklapanja i bez rupa, nijedan deo kuke ne sme da izađe van pravougaonika, i kuke smemo slobodno okretati i prevrtati.
Rešenje:
Pravougaonik se može pokriti u samo sledećim slučajima:
1)
,
;
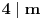
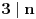
2)
,
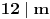
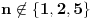
(ili isto ovo sa zamenjenim
).
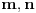
Pretpostavimo da je neki
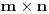
pravougaonik već pokriven na opisani način. Najpre uočimo da svakoj kuki možemo pridružiti neku drugu koja pokriva njeno „unutrašnje“ polje. Pri tome je očigledno da je ovakvo pridruživanje uzajamno, tj. da smo time podelili skup kuka na parove tako da svaki par obrazuje jednu od sledeće dve
pločice.
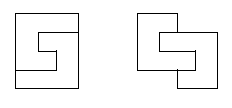
Pošto se svaka pločica sastoji od
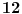
jediničnih kvadrata, odmah zaključujemo da
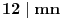
. Pretpostavimo da je jedan od
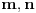
deljiv sa
, i neka, bez umanjenja opštosti,
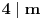
. Ako pri tome i
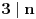
, polazni pravougaonik možemo razbiti na pravougaonike veličine
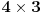
, od kojih svaki možemo lako pokriti.
Dalje, ako
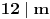
i
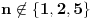
, uvek postoje
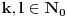
takvi da je
(
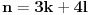
rezultat Silvestera) pa u tom slučaju pravougaonik izdelimo na delove
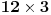
i
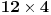
od kojih svaki možemo pokriti kao što je već pokazano, a u slučaju
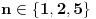
očigledno je da traženo pokrivanje ne postoji.
Preostao nam je još slučaj
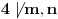
. Tada su
i
parni brojevi, a broj pločica je neparan. Obojmo svaku četvrtu kolonu u crno, svaki četvrti red u crno, a preseke ovih obojenih redova nećemo obojiti. Primetimo da svaka pločica pokriva neparan broj obojenih kvadratića i ima ih neparan broj, a ukupno ima parno obojenih kvadratića. Kontradikcija.
Ljubičice crvena, što si plava kô zelena trava.
zadatak sa olimpijade
Registrovani: 1 ( Pirate )