Zadatak sa dva suprotna rešenja- Dokazati da se u krug poluprečnika 1 može smestiti 2*2006 krugova, tako da nijedan krug nema zajedničku unutrašnju tačku sa ostalim krugovima, a da im je zbir poluprečnika jednak 2006.
Ovaj zadatak ima dva SUPROTNA rešenja, jedno kojim se dokazuje tvrđenje, a jedno kojim se to tvrđenje obara. Oba rešenja izgledaju logično i tačno, ali sigurno je da ne mogu biti oba tačna, pa vas molim za pomoć da nađemo koje je pogrešno. Evo kako idu rešenja
1: U krug poluprečnika 1 može se upisati kvadrat stranice
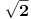, pa samim tim i kvadrat stranice 
. Ako taj kvadrat izdjelimo na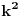 
kvadrata, stranica 
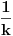i u njih upišemo krugove, poluprečnici tih krugova će biti 
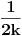. Ako uzmemo da je zbir poluprečnika, prema uslovu iz zadatka, jednak 2006, dobijamo:
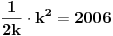, tj.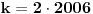
, iz čega sledi da se može smestiti 2006*2 krugova da im je suma poluprečnika 2006.Ovo je, inače, bilo zvanično rešenje komisije.
2: Ako uzmemo da postoje ti krugovi i označimo ih sa
, a prvi (dati) krug sa 
onda je: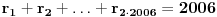
.Da bi manji krugovi bili smesteni u veći, dati krug, mora da je zadovoljeno:
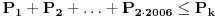
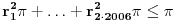
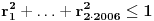.Koristeci nejednakost kvadratne i aritmeticke sredine dobijamo:
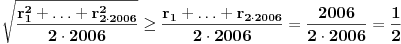, tj.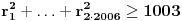
, sto je u kontradikciji sa 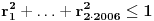, pa krugovi ne mogu postojati.Ovo je bilo moje resenje zadatka, na koje sam dobio max. 25 poena, ali bih da resim dilemu koje je resenje ispravno.
Re: Zadatak sa dva suprotna rešenja