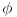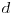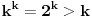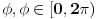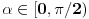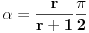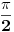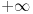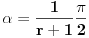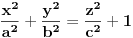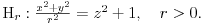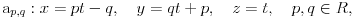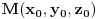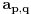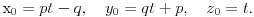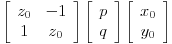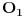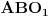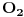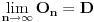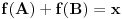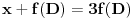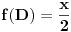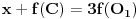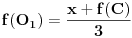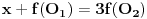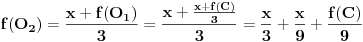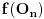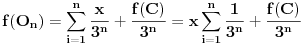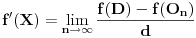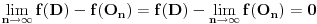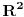BRAAAAAVOOOOO, BRAAAAVIIISIIIMOOOOOOOOO!
Sve čestitke Filipu za rešenje. Čak je idejno identično onom koje sam hteo da postujem. Ipak, Filopvo rešenje ima jedan mali bagčić. Naime, ugao bi trebao da opada od
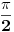
do 0 kada r raste od 0 do
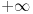
da se "dvostruke kragne" ne bi sekle. Može se koristiti na primer veza
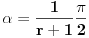
. To je sve što imam da ispravim u Filipovom rešenju. E pa Filipe, svaka ti čast, nemam šta drugo da kažem (tj. napišem).
Inače, površ čija je kanonska jednačina
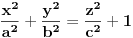
se zove jednograni (ili eliptički) hiperboloid. Filipova "dvostruka kragna" je zapravo kružni hiperboloid, tj. specijalan slučaj čija je kanonska jednačina

. Inače, jedan moj drug zove jednograni hiperboloid "kukić strukić"!
Jednograni hiperboloid ima sledeće fundamentalno svojstvo: Kroz svaku tačku jednogranog hiperboloida prolaze tačno dve prave koje cele leže na tom hiperboloidu. Zato ga možemo predstaviti kao uniju disjunktnih pravih. To se još izražava rečima: "Jednograni hiperboloid je 2-mnogostrukost". Upućeniji ne treba da pojam n-mnogostrukosti pomešaju sa pojmom n-dimenzione mnogostrukosti. To su potpuno različiti pojmovi.
Dovoljno je sada da izaberemo po jednu pravu kroz svaku tačku na npr. malom krugu te površi (od kojega je Filip pošao) povučemo jednu od tih pravih, ali da ih uvek "češljamo" na istu stranu.
Sada se ceo prostor bez izabrane prave p može predstaviti kao disjunktna unija kružnih hiperboloida sa osom p, a svaki od njih kao disjunktna unija pravih. Jasno je da će sve one biti međusobno disjunktne, kao i da su mimoilazne sa p. No, da dve prave iz disjunktnih hiperboloida sa istom osom p nikada ne bi bile paralelne, potrebno je da se u navedenom kanonskom obliku isti količnik r/c ne
"ponovi dvaput".
Planirao sam da postujem sledeću familiju hiperboloida:
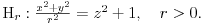
Tada bi se kao odgovarajuća familija pravih dobila familija pravih
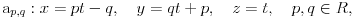
datih u parametarskom obliku. Veza između parametara p,q i r data je sa

. Za p=q=0 se dobija zajednička osa svih tih kružnih hiperboloida. To je ona prava koja se na kraju dodaje.
Hajde da direktno proverimo da ova familija pravih ispunjava tražene uslove. Neka je
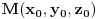
proizvoljna tačka prostora. Da bi tačka M pripadala pravoj
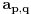
potrebno je i dovoljno da za neko t važi
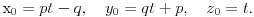
No, za t i nemamo mnogo izbora, pa zapravo treba da važi

ili u matričnom obliku
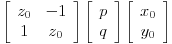
To je sistem od dve linearne jednačine po p i q sa determinantom

koja je uvek različita od nule, pa imamo jedinstveno rešenje po p i q. Drugim rečima, svaka tačka prostora pripada tačno jednoj od pravih iz naše familije.
To znači da smo pokupili sve tačke prostora i da su sve prave iz te familije disjunktne. Treba samo još proveriti da nikada nisu paralelne (jer se zbog disjunktnosti ne mogu seći). No, vektor prave
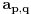
je (p,q,1), a vektori (p,q,1) i (p',q',1) su kolinearni ako i samo ako je p=p' i q=q', čime je dokaz završen.
Još jednom sve čestitke za Filipa, a ja bih samo još da naglasim da sam svoj prethodni post pisao dok je Filip slao svoje rešenje, pa u trenutku slanja posta nisam znao da je nako u međuvremenu dostavio rešenje.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.




 Popunjavanje prostora i podela ravni.
Popunjavanje prostora i podela ravni.