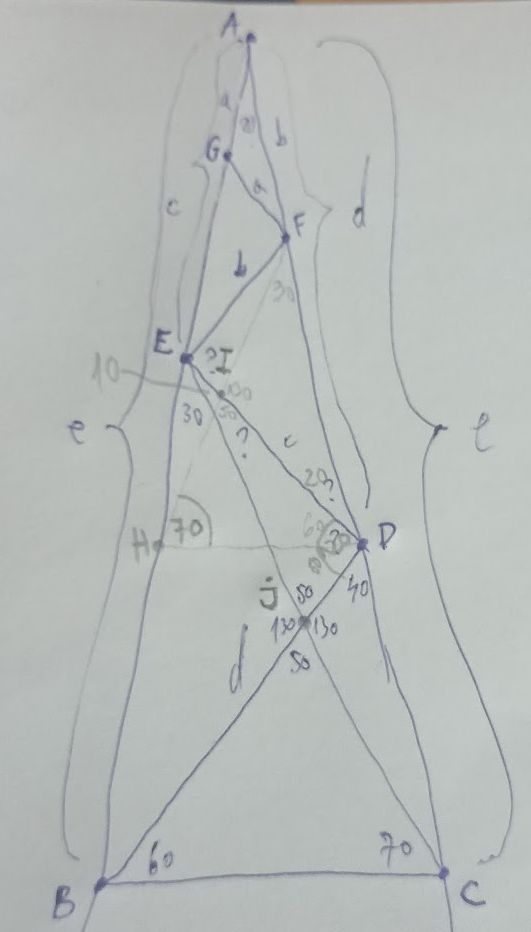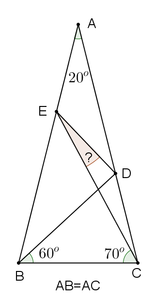
Date su tačke E i D na kracima AB i AC, jednakokrakog trougla ABC, takve da je
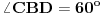 i
i 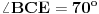 . Odrediti ugao
. Odrediti ugao 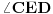 , ako je ugao naspram osnovice trougla 20o.
, ako je ugao naspram osnovice trougla 20o.Zadatak može da se reši pomoću trigonometrije. Ne znam da li je moguće zadatak rešiti pomoću Euklidske geometrije.




 Treći zadatak sa uglovima
Treći zadatak sa uglovima