[es] - Kupa i presek prave i kupe pod raznim uglovima

Juhas

Član broj: 50387
Poruke: 4
*.dial.InfoSky.Net.

Profil

Kupa i presek prave i kupe pod raznim uglovima

^{03.03.2005. u 11:38 - pre 244 meseci}

Hitno mi je potrebno resenje zadataka sa presekom kupe i prave pod raznim uglovima, tako da se dobije krug, parabola, hiperbola i elipsa. Ko zna ovo, molio bih ga/je da mi pomogne!

Odgovor na temu

lampica
Bg

Član broj: 31577
Poruke: 109
*.frikom.co.yu.

ICQ: 334198593
Sajt: www.skoladekart.com

Profil

Re: Kupa i presek prave i kupe pod raznim uglovima

^{03.03.2005. u 14:36 - pre 244 meseci}

Citat:

Juhas: Hitno mi je potrebno resenje zadataka sa presekom kupe i prave pod raznim uglovima, tako da se dobije krug, parabola, hiperbola i elipsa.

Bilo bi dobro da nam kažeš o kakvim se zadacima radi, ovo što si napisao teško da može da posluži bilo kome da ti pomogne.

Verovatno misliš na neke preseke kupe i ravni, s obzirom da presek kupe i prave u najboljem slučaju daje pravu (i još 2, 1 ili nijednu tačku)?

Odgovor na temu

KPYU
Karan Predrag

Član broj: 36769
Poruke: 143
*.beotel.net.

Profil

Re: Kupa i presek prave i kupe pod raznim uglovima

^{03.03.2005. u 22:50 - pre 244 meseci}

Zamisli da imaš pravu kružnu kupu. Neka sve izvodnice prolaze kroz teme V i zaklapaju isti ugao

sa osom o.

Bilo koja ravan koja ne sadrži V i normalna je na o seče kupu po kružnoj liniji

Bilo koja ravan koja ne sadrži V i zaklapa ugao sa osom ugao

seče konus po elipsi.

Bilo koja ravan koja ne sadrži V i zaklapa ugao sa osom ugao

seče konus po paraboli.

Bilo koja ravan koja ne sadrži V i zaklapa ugao sa osom ugao

seče konus po hiperboli.

Takođe bilo koja ravan koja ne sadrži V i paralelna je sa osom seče ugao po hiperboli.

Odgovor na temu

Juhas

Član broj: 50387
Poruke: 4
*.dial.InfoSky.Net.

Profil

Re: Kupa i presek prave i kupe pod raznim uglovima

^{04.03.2005. u 06:59 - pre 244 meseci}

Presek kupe i ravni mi takodje moze puno pomoci! Npr. Ako ravan sece kupu pod pravim uglom, kada se dobije krug, trebaju mi sledeci zadaci - Kako se povecava ili smanjuje visina na kojoj ravan sece kupu, povecava se i obim, povrsina kruga. Ista vrsta zadataka mi treba i za hiperbolu, parabolu i elipsu. Mozda znate neke sajtove na kojima mogu naci i besplatno download-ovati programe koji resavaju zadatke sa kupama, elipsama, ...

Prikačeni fajlovi

Slike.zip - 8.2k

Odgovor na temu

KPYU
Karan Predrag

Član broj: 36769
Poruke: 143
194.106.165.*

Profil

Re: Kupa i presek prave i kupe pod raznim uglovima

^{04.03.2005. u 18:12 - pre 244 meseci}

Ej, 'ajde formuliši zadatak, da ne bi bilo nešto poput "Ima li iko pojma o bilo čemu, i da li to inakoji način može da formuliše?"

Mislim, da li radiš analitičku, projektivnu, nacrtnu, deskriptivnu ili diferencijalnu geometriju.

Btw ja sam ti pričao o preseku konusa & ravni, jer to je kriva. Presek konusa i prave je ili prazan skup ili tačka ili 2 tačke ili cela prava.

Šta imaš da računaš oko tačke? Da li njene koordinate ? Ako je tako, koja ti je jednačina konusa, koja jednačina prave etc etc etc

Odgovor na temu

Juhas

Član broj: 50387
Poruke: 4
*.dial.InfoSky.Net.

Profil

Re: Kupa i presek prave i kupe pod raznim uglovima

^{05.03.2005. u 15:12 - pre 244 meseci}

Radim analiticku geometriju.
Prilikom preseka kupe i prave mi trebaju koordinate tacki, jednacina prave koja se dobije... (KAKO DA IH IZRACUNAM!). A, prilikom preseka kupe i ravni mi trebaju jednacine kruga, elipse, hiperbole, i parabole, i to na sledeci nacin:
da li se, i kako povecava, odnosno smanjuje vrednost jednacine kruga, parabole,... kada ravan sece kupu blize bazi, i blize vrhu kupe.
Trebaju mi takvi zadaci i dokazi da se povecava i smanjuje vrednost jednacine kruga, parabole,... kada ravan sece kupu blize vrhu kupe, ili blize samoj bazi.
Nemam precizan zadatak. Sam zadatak mi je da ovo dokazem preko nekih formula, izracunavanja... Ili da predstavim program koji ovo radi. Ako znas neki program koji mogu besplatno skinuti sa Interneta, postavi link.

Odgovor na temu

KPYU
Karan Predrag

Član broj: 36769
Poruke: 143
*.beotel.net.

Profil

Re: Kupa i presek prave i kupe pod raznim uglovima

^{06.03.2005. u 02:00 - pre 244 meseci}

Što se tiče preseka prave i bilo koje površi, moraš imati jednačinu prave (po mogućstvu u parametarskom obliku) i jednačinu površi. Zameni koordinate iz prave u površ i dobije kvadratnu jednačinu po parametru koja ima 2, 1 ili 0 rešenja. Zameni taj parametar (te parametre) i dobijaš tačku (tačke) preseka.

Što se tiče preseka ravni i konusa upotrebi linearne ortogonalne smene. Tako, ako te zanima uopšteno bilo koji konus, nj jednačina je

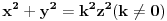
. Kod njega je ugao između izvodnica (bilo koje) i ose

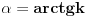
Neka je jednačina ravni ax + by + cz + d =0. Ona sa osom zaklapa ugao

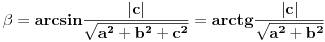
Ako je d=0, ravan prolazi kroz teme, pa je presek tačka (konkretno teme), prava (konkretno neka izvodnica) ili dve prave (dve izvodnice), u zavisnosti da li

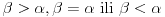
Ako je a=b=0 to je krug.

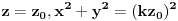
U protivnim smena

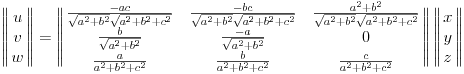
Objašnjenje:
- Treća vrsta ti je vektor ravni (samo normiran tj podeljen svojom dužinom). Uzimamo vektor ravni da bi promenljiva w bila broj.
- Druga vrsta je vektor u ravni koji je normalan na osu konusa. To će biti osa našeg preseka
- Prva vrsta je vektor normalan na vektor ravni (<=> pripada ravni) i na vektor normalan na osu konusa. To znači da je ovaj vektor normalna projekcija vektora ose na ravan. To će biti glavna osa naše krive
- Normiramo da bi bilo lakše naći P^-1. Naime ovako je P^-1 = P^T

Smenu možemo zapisati u skraćenom obliku U=PX. Tada je X=P^TU. (Transponat od P. P je zapisana gore) Zameni u jednačine konus i prave i dobijaš (nemoj me držati za reč, proveri)

.

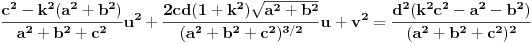
Dalje, pretpostavljam, možeš sam.

Odgovor na temu