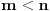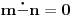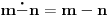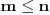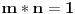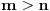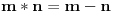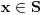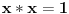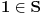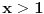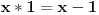Citat:
XDarko: A za primer beskonacnog podrupoida mozemo uzeti recimo skup prirodnih parnih brojeva...
Ovaj deo je nepotreban jer se nigde ne traži da grupoid uopšte ima prave podgrupoide. Ako bi zadatak glasio "Naći beskonačan grupoid koji ima prave podgrupoide, ali nijedan od njih nije konačan", onda bi ovo zaista bilo potrebno.
Ovako kako je zadatak postavljen, za oba dela zadatka dovoljno je bilo naći beskonačan grupoid bez pravog podgrupoida. Primer je grupoid na skupu prirodnih brojeva sa binarnom operacijom * definisanom na sledeći način:
Ako je m različito od n, onda je m*n=1, dok je m*m=m+1.
Za deo pod b) si u pravu. Moja greška. Ako želimo primer beskonačnog grupoida sa pravim podgrupoidima, ali pri čemu su svi oni konačni, možemo izabrati skup prirodnih brojeva sa nulom sa operacijom

(koja se yove "monus") definisanom na sledeći način: Ako je
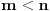
, onda je
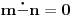
, a u protivnom je
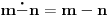
.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.




 Teorija grupa...
Teorija grupa...