Rimanov integral se definiše na domenima merljivim po Žordanu, recimo pozitivne mere i postoji akko je podintegralna funkcija ograničena i ima skup tačaka prekida Lebegove mere nula. Dakle, za ma koje
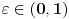
Rimanov integral date funkcije na intervalu
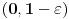
, koji je merljiv po Žordanu.
U slučaju Lebegovog integrala, nesvojstveni integral se ne definiše, jer Lebegov integral nema problem sa singularitetima. Svaki apsolutno konvergentan nesvojstveni integral postoji kao običan Lebegov integral.
Smenu
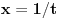
nisi uvela dobro. Izložilac treba da ti bude manji za jedan.
Dalje, probaj parcijalnom integracijom integrala
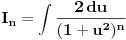
da odrediš vezi između

i
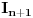
, a onda izrazi
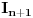
preko

.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
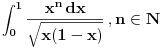 .
.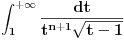 , pa tu uvedem smenu
, pa tu uvedem smenu 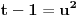 i dobijem
i dobijem 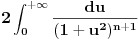 . Onda uvedem smenu u = tg v i dobijem
. Onda uvedem smenu u = tg v i dobijem 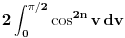 . Cisto ako neko moze da mi kaze da li mi valja postupak i sta dalje.
. Cisto ako neko moze da mi kaze da li mi valja postupak i sta dalje.