Citat:
berazorica:
Šta bi Bojan rekao kad bi mu student na ispitu iz geometrije zadatak rešio metodama analitičke geometrije? Ili su zadaci baš tako pažljivo odabrani, da je to nemoguće?
Prihvatio bih rešenje, naravno — štaviše, uz pohvalu studentu (uvek mi je
drago kada neko reši zadatak drugačije nego što sam predvideo). A drugo je pitanje da li mi se to nekad desilo u praksi: nije (mada nešto donekle slično jeste, biće reči o tome pri kraju poruke). Kako to da se navedeni primer nikada nije desio? Zadaci
nisu tako pažljivo odabrani da je rešenje putem analitičke geometrije nemoguće — u stvari, kada biram zadatke za kolokvijum, priznajem da i ne pomišljam na to koliko bi rešenje putem analitičke geometrije bilo komplikovano. No, ipak, analitička geometrija je malo specifična: iako se putem nje se može rešiti recimo 70% geometrijskih zadataka, verovatno je u 95% takvih primera rešenje neuporedivo složenije nego rešenje putem elementarne geometrije (procenti su odokativno navedeni, ali mislim da je suština jasna).

To može biti jedno objašnjenje kako to da još nisam dobio rešenje zadatka putem analitičke geometrije. No, bojim se da postoji i drugačije: nažalost, stičem utisak da je šablonizacija matematike u glavama studenata sve izraženija (za šta ne kažem da su sami odgovorni, bar ne sasvim — dobar deo krivice jeste na onima oni koji na šablonski način predaju raznorazne predmete, a da pritom sve to može i mnogo drugačije). Prosto, student maltene svaki predmet doživljava kao gomilu šablona koje treba da nabifla napamet, i kad ga jednom položi — e, onda mora da isprazni glavu od tih šablona, kako bi u nju stali šabloni za sledeći predmet. (Naravno, ni slučajno ne tvrdim da ovo važi za
sve studente. Samo ističem pojavu koja deluje da sve više uzima maha.)
Baš mi u toku pisanja ove poruke pade na pamet jedan baš upečatljiv primer. Održavan je prijemni ispit za
doktorske studije matematike, i bio je jedan geometrijski zadatak. Ispostavilo se da je taj geometrijski zadatak „dušu dao“ za rešavanje analitičkom metodom (naravno, postojalo je i vrlo pristojno elementarno rešenje, čak više različitih, ali se prosto uklopilo tako da i analitička geometrija rešava zadatak očas posla). Apsolutno svi koji su rešili zadatak rešili su ga elementarnim putem. I posle prijemnog razgovara jedna studentkinja koja nije prošla prijemni, ali joj je malo falilo, s jednim članom komisije za pregled zadataka s tog prijemnog. Ta studentkinja nije rešila pomenuti zadatak. Pomenuti profesor joj pokazuje razne načine za rešavanje, i dodaje: „A i ako ti nije palo na pamet ništa od ovoga, mogla si bar pokušati analitičkom geometrijom, evo vidi koliko se brzo stigne do rešenja“. Studentkinja, sva zatečena ovim poslednjim komentarom, dodaje: „A to je
smelo da se radi??!!“ Dakle, naglašavam još jednom, u pitanju je prijemni za
doktorske studije, pomenuta studetkinja je vrlo dobra (kasnije je i položila prijemni, u drugom krugu, i trenutno je na doktorskim studijama) — pa je sva šokirana saznanjem da se geometrijski zadatak
sme rešavati i analitičkim putem!
No, svrh svega mislim da primer analitičke geometrije i nije baš u skladu s temom. Ovde je zadatak bio rešavanje limesa uz zabranu primene Lopitalovog pravila, a da je pri tome Lopitalovo pravilo rađeno iz
istog predmeta, čak u
istoj tematskoj celini (izračunavanje graničnih vrednosti), i zabranjeno je jedino iz razloga što vodi do rešenja u dva reda! Rekoh ranije: sigurno nije loša ideja proveriti na kolokvijumu ume li student da rešava limese na neki drugi način, a ne primenom Lopitalovog pravila. Ali onda mu lepo daj limes koji
mora da rešava na drugi način — tako ćeš em postići šta si hteo (proveriti ume li se on snaći i bez Lopitalovog pravila), em će studentu biti jasno zašto on treba da zna i druge stvari pored Lopitalovog pravila (zato što postoje limesi za koje Lopitalovo pravilo nije bogomdano — dok se, nasuprot tome, u primeru iznetom u temi studentu maltene šalje poruka da Lopitalovo pravilo funkcioniše uvek, ali da za neke limese asistent/profesor prosto „’oće nešto drugo“?!). Pravi geometrijski pandam ovakvom primeru bio bi kada bih na ispitu zahtevao od studenata da reše neki zadatak, ali bez korišćenja Pitagorine teoreme. Duhovito.
Uglavnom, evo onog primera koji sam najavio na samom početku. Jednom prilikom zadao sam ovakav zadatak: bila je data kružnica
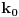
, nešto se u njoj dešavalo, i tu je trebalo nešto dokazati (nisu sad bitni detalji). Uglavnom, moja ideja je bila da se uoči sledeće: ukoliko kružnicu
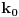
zamislimo kao apsolutu Poenkareovog modela, svi drugi posmatrani objekti imaju svoju interpretaciju kao određeni hiperbolički pojmovi, i ispostavlja se da je postavka zadatka zapravo prepričavanje, u Poenkareovom modelu, određenog zadatka iz hiperbolične geometrije urađenog na vežbama. Kako Poenkareov model predstavlja model hiperbolične geometrije, sve što važi u hiperboličnoj geometriji važi i u njemu, te tvrđenje zadatka sledi iz tvrđenja dokazanog na vežbama. Ta konstatacija bila je sve što sam ja očekivao kao rešenje zadatka. Neki studenti su to i primetili, i dobili maksimalan broj bodova. No, jedna studentkinja to nije primetila, već je zadatak rešavala na potpuno euklidski način, i posle ispisane dobre tri strane zaista dokazala ono što se tražilo.
Naravno, i ona je dobila maksimalan broj bodova, i još sam je jednom kasnijom prilikom pohvalio, uz napomenu da mi je veoma drago što je demonstrirala da se zadatak može rešiti i tako. Je li ona tu pokazala neko znanje iz hiperbolične geometrije (budući da je zadatak bio zamišljen da bude iz te oblasti)? Očigledno nije pokazala ni da zna da postoji hiperbolična geometrija, a kamoli kako ona izgleda (naravno, ja ne tvrdim da ona to ne zna, samo se prosto iz njenog rešenja ne može ama baš ništa reći o tome). Je li ona tu pokazala da ume razmišljati svojom glavom?
Apsolutno jeste. Pritom, hiperboličnu geometriju će najverovatnije svakako brzo zaboraviti, a sposobnost matematičkog načina razmišljanja će imati doveka. Zato je ovo drugo i jedino što me zanima kod studenata.
Ljubičice crvena, što si plava kô zelena trava.