• Naslovna
• FAQ
• Pravilnik
• O ES-u
• Tim
• Korisnici
• Statistike

 

• elitesecurity ::
• elitemadzone ::
• EMAIL ::
• RSS ::
• ES Mobile

  Niste ulogovani?  Username :   Password:   

• Registracija
• Zaboravili ste password?
• Flashback ▲▼
• Login problem?

 

Pretraga:

 

Srodne teme Kliknite za generisanje liste srodnih tema... Navigacija Brisanje liste Aktuelne teme u ovom forumu: Još jedan zadatak sa uglovima Treći zadatak sa uglovima Ostala rešenja algebarske jednačine Lep zadatak sa uglovima Najmanje pozitivno realno r Ikosaedar i gustina ms matematika.... Jedan zadatak sa pravouglim trouglom Japanese | Can you solve this ? | Math.. Jednakostraničan trougao Logaritamska nejednakost Raspoređivanje slova Košarkaši lep zadatak Zanimljiv zadatak o uglovima trougla Stado Boga Sunca ... 2000 godina star .. Izaberite forum: Linux Linux aplikacije Linux desktop okruženja Linux hardware Windows desktop Windows aplikacije Zaštita Office Windows drajveri Office :: Word Office :: Excel Macintosh Mac hardware Mac software Iphone Enterprise Networking SOHO Networking Wireless Windows mreže Linux mreže Wireless :: WiMax Wireless :: Mikrotik Wireless :: Wireless oprema Linux/UNIX serveri i servisi Unix BSD Skript jezici Security Virtualizacija Cloud Computing Services Security :: Kriptografija i enkripcija .NET 3D programiranje Art of Programming Asembler C/C++ programiranje Kernel i OS programiranje Pascal / Delphi / Kylix Java Embedded sistemi Perl PHP Python Visual Basic 6 Veštačka inteligencija Security Coding XML GameDev - Razvoj Igara Ostali programski jezici PHP :: PHP za početnike PHP :: Smarty template engine .NET :: .NET Desktop razvoj .NET :: ASP.NET .NET :: WPF Programiranje C/C++ programiranje :: C/C++ za početnike Baze podataka MySQL Oracle Access MS SQL Firebird/Interbase PostgreSQL Fiksna telefonija VoIP Udruženje korisnika teleko.. GSM - telefoni GSM - upotreba GSM - servisiranje Mreže i novosti Smartphone Mreže i novosti :: Mobilni internet Mreže i novosti :: Telenor - korisnički servis Mreže i novosti :: VIP - korisnički servis Mreže i novosti :: MTS - korisnički servis Smartphone :: Symbian OS Smartphone :: Windows Mobile Smartphone :: Android GSM - telefoni :: Nokia PDA Uređaji GPS Portable Players Anonimnost i privatnost ISP Browseri E-mail Instant Messaging FTP Google Hosting ISP :: Wireless mreže i ISP ISP :: ADSL E-mail :: Anti-spam Instant Messaging :: IRC Hosting :: Domeni Google :: Gmail E-Marketing Web aplikacije Web dizajn i CSS Web dizajn softver Web razvoj Pretraživači i SEO Flash Javascript i AJAX Web dizajn i CSS :: Kritike Grafički dizajn Izdavaštvo 3D modelovanje Rasterska grafika Vektorska grafika 3D modelovanje :: CAD/CAM Matične ploče, procesori .. Video karte i monitori Storage Ostali hardver Overclocking & Modding PC Konfiguracije Laptopovi Vodič za kupovinu - PC har.. Tablet PC Muzička produkcija Audio kompresija Audio softver Video produkcija Video kompresija Video softver Multimedijalni uređaji Digitalni fotoaparati Digitalne kamere Home Theater Digitalni fotoaparati :: Fotografija Digitalni fotoaparati :: Vodič za kupovinu - Digita.. Elektronika Elektrotehnika Elektronika :: TV uređaji Elektronika :: Radio elektronika i tehnika Elektronika :: Mikrokontroleri Elektronika :: Audio-elektronika Auto-elektronika :: Tuning Vodič za učenje Vodič za posao Vodič za emigraciju Fizika Matematika Nauka Sertifikati Informatika Vodič za učenje :: Seminarski radovi Vodič za učenje :: Obrazovne institucije Vodič za emigraciju :: Život u USA Vodič za emigraciju :: Život u Norveškoj Vodič za emigraciju :: Život u Nemačkoj E-Poslovanje E-Kupovina IT pravo i politika razvoja IT događaji IT berza poslova IS i ERP Ekonomija Berza Cryptocoins IT berza poslova :: Arhiva IT berze poslova IT pravo i politika razvoja :: Registar Nacionalnog ID E-Poslovanje :: E-Transakcije E-Poslovanje :: Forex E-Kupovina :: Platne kartice Digitalna Televizija Advocacy Ankete Predlozi i pitanja Vesti Čekaonica Vesti :: ES leto manifestacija MadZone TechZone Poljoprivreda AutoZone MotoZone Svakodnevnica Video igre MadZone :: Zanimljivi linkovi MadZone :: Kultura TechZone :: Ergonomija TechZone :: Grejanje TechZone :: Klimatizacija TechZone :: Bela tehnika AutoZone :: Fiat Panda club Lista poslednjih: 16, 32, 64, 128 poruka.

jovanrisitc Elektronski fakultet Nis Nis Član broj: 196352 Poruke: 7 212.200.65.* Profil Geomatrija_Problematican_Zadatak 04.12.2010. u 11:13 - pre 175 meseci Prava deli trougao na dva dela jednakih povrsina i obima. Dokazati da prolazi kroz centar upisanog kruga. Pomoc bi mi zaista dobrodosla, vec duze se mucim. Unapred hvala. Odgovor na temu

Sini82 Član broj: 234605 Poruke: 479 62.101.141.* Jabber: Sini82@elitesecurity.org +33 Profil Re: Geomatrija_Problematican_Zadatak 04.12.2010. u 15:53 - pre 175 meseci Prava siječe trougao na dva dijela od kojih je uvijek bar jedan od njih trougao. Dokaz ne gubi na opštosti ako pretpostavimo da prava siječe stranice trougla AB i BC redom u tačkama D i E. Nađimo presjek simetral ugla kod tjemena B i duži DE, označimo ga sa F. 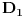Spustimo normale iz tačke F na stranice AB i BC i označimo podnožja njihovih normala redom sa i . 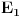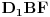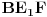Na osnovu podudarnosti trouglova i dobijamo da vrijedi . 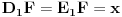tj. . . . 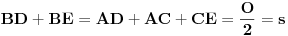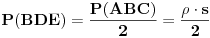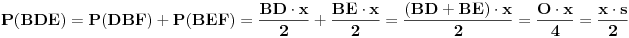Iz poslednje dvije jednakosti slijedi . 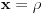Na osnovu konstrukcije tačke F, zaključujemo da se podudara sa centrom upisane kružnice u trougao (tačkom u kojoj se sijeku simetrale uglova trougla), što je i trebalo dokazati. Odgovor na temu

jovanrisitc Elektronski fakultet Nis Nis Član broj: 196352 Poruke: 7 *.dynamic.isp.telekom.rs. Profil Re: Geomatrija_Problematican_Zadatak 04.12.2010. u 16:14 - pre 175 meseci Hvala puno na ovako lepom resenju. Odgovor na temu