Evo, u čemu je stvar:
Najpre sam hteo da nađem algebarsku interpretaciju Paskalove teoreme i dokažem je na algebarski način. Radio sam u homogenim koordinatama. Uslov da vektor koji predstavlja tačku i vektor koji predstavlja pravu odgovaraju incidentnim objektima (tačka pripada pravoj) je zapravo ortogonalnost vektora homogenih koordinata (tačke i prave). Stoga se vektor koji predstavlja pravu kroz dve tačke može dobiti kao vektorski proizvod (u R
3, gde leže vektori homogenih koordinata) vektora koji predstavljaju tačke, tj AB = A x B. Slično tome je presečna tačka pravih zapravo predstavljena vektorskim proizvodom vektora kojima su predstavljene prave. Uslov kolinearnosti triju tačaka i konkurentnosti triju pravij je jednakost mešovitog proizvoda nuli, tako da je algebarski zapis Paskalove teoreme
.
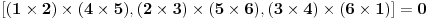
Odnosno nakon primene formula za dvostruki vektorski proizvod
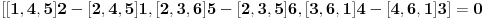
ili posle sređivanja
(*)
.
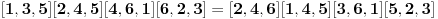
Dakle, ovu jednskost treba dokazati. Pretpostavimo da su tačke 1,...,5 fiksne, a da tačka 6 ima opšte koordinate
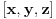
. (*) je algebarska jednačina najviše drugog reda po
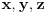
. Ona je ili trivijalna jednačina 0=0 (koja je svakako tačna) ili jednačina nekog konusnog preseka, degenerisanog ili nedegenerisanog. Lako se pokayuje da se zamenom tačke 6 bilo kojom od tačaka 1,...,5 dobija identitet, to jest, sve od tačaka 1,...,5 zadovoljavaju jednačinu (*), pa je (*) ili trivijalna jednačina 0=0 ili jednačina konusnotg preseka (degenerisanog ili nedegenerisanog), koji sadrži tačke 1,...,5. U slučaju degenerisane konike, među bilo kojih njenih pet tačaka mogu izabrati tri kolinearne, dok nedegenerisan konusni presek nema trojki kolinearnih tačaka. Stoga, pošto tačke 1,...,5 leže na nedegenerisanom konusnom preseku od koga smo pošli, među tačkama 1,...,5 nema triju kolinearnih, pa ako jednačina (*) nije trivijalna, onda je to jednačina nedegenerisanog konusnog preseka koji prolazi kroz tačke 1,...,5. Ukoliko je takav konusni presek jedinstven, onda je to naš polazni konusni presek, kome pripada i tačka 6, pa samim tim važi (*).
Zašto me ovo zanima? Pa, da bih pokušao da nađem uopštenja Paskalove teoreme, na primer za n-dimenzioni slučaj ili neka druga.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
Konusni presek kroz 5 tačaka
Registrovani: 0 ( 0 )
