• Naslovna
• FAQ
• Pravilnik
• O ES-u
• Tim
• Korisnici
• Statistike

 

• elitesecurity ::
• elitemadzone ::
• EMAIL ::
• RSS ::
• ES Mobile

  Niste ulogovani?  Username :   Password:   

• Registracija
• Zaboravili ste password?
• Flashback ▲▼
• Login problem?

 

Pretraga:

 

Srodne teme 11.12.2001. Paskal, nije mi jasno... 10.09.2002. nizovi & nizovi 04.11.2004. Klase i nizovi (pocetnicko pitanje) 21.02.2005. Aritmeticki i geometrijski niz 27.04.2005. nizovi i dvostruka preciznost? 13.06.2005. Aritmeticki niz - pomoc 01.02.2006. nizovi i trigonometrija 27.06.2006. Kako se zovu ovi nizovi? 26.01.2007. Nizovi, max,min pocetnicki problemi!!!! 29.05.2007. vbnet polja i nizovi, ima li neke razlike Navigacija Brisanje liste Aktuelne teme u ovom forumu: Još jedan zadatak sa uglovima Treći zadatak sa uglovima Ostala rešenja algebarske jednačine Lep zadatak sa uglovima Najmanje pozitivno realno r Ikosaedar i gustina ms matematika.... Jedan zadatak sa pravouglim trouglom Japanese | Can you solve this ? | Math.. Jednakostraničan trougao Logaritamska nejednakost Raspoređivanje slova Košarkaši lep zadatak Zanimljiv zadatak o uglovima trougla Stado Boga Sunca ... 2000 godina star .. Izaberite forum: Linux Linux aplikacije Linux desktop okruženja Linux hardware Windows desktop Windows aplikacije Zaštita Office Windows drajveri Office :: Word Office :: Excel Macintosh Mac hardware Mac software Iphone Enterprise Networking SOHO Networking Wireless Windows mreže Linux mreže Wireless :: WiMax Wireless :: Mikrotik Wireless :: Wireless oprema Linux/UNIX serveri i servisi Unix BSD Skript jezici Security Virtualizacija Cloud Computing Services Security :: Kriptografija i enkripcija .NET 3D programiranje Art of Programming Asembler C/C++ programiranje Kernel i OS programiranje Pascal / Delphi / Kylix Java Embedded sistemi Perl PHP Python Visual Basic 6 Veštačka inteligencija Security Coding XML GameDev - Razvoj Igara Ostali programski jezici PHP :: PHP za početnike PHP :: Smarty template engine .NET :: .NET Desktop razvoj .NET :: ASP.NET .NET :: WPF Programiranje C/C++ programiranje :: C/C++ za početnike Baze podataka MySQL Oracle Access MS SQL Firebird/Interbase PostgreSQL Fiksna telefonija VoIP Udruženje korisnika teleko.. GSM - telefoni GSM - upotreba GSM - servisiranje Mreže i novosti Smartphone Mreže i novosti :: Mobilni internet Mreže i novosti :: Telenor - korisnički servis Mreže i novosti :: VIP - korisnički servis Mreže i novosti :: MTS - korisnički servis Smartphone :: Symbian OS Smartphone :: Windows Mobile Smartphone :: Android GSM - telefoni :: Nokia PDA Uređaji GPS Portable Players Anonimnost i privatnost ISP Browseri E-mail Instant Messaging FTP Google Hosting ISP :: Wireless mreže i ISP ISP :: ADSL E-mail :: Anti-spam Instant Messaging :: IRC Hosting :: Domeni Google :: Gmail E-Marketing Web aplikacije Web dizajn i CSS Web dizajn softver Web razvoj Pretraživači i SEO Flash Javascript i AJAX Web dizajn i CSS :: Kritike Grafički dizajn Izdavaštvo 3D modelovanje Rasterska grafika Vektorska grafika 3D modelovanje :: CAD/CAM Matične ploče, procesori .. Video karte i monitori Storage Ostali hardver Overclocking & Modding PC Konfiguracije Laptopovi Vodič za kupovinu - PC har.. Tablet PC Muzička produkcija Audio kompresija Audio softver Video produkcija Video kompresija Video softver Multimedijalni uređaji Digitalni fotoaparati Digitalne kamere Home Theater Digitalni fotoaparati :: Fotografija Digitalni fotoaparati :: Vodič za kupovinu - Digita.. Elektronika Elektrotehnika Elektronika :: TV uređaji Elektronika :: Radio elektronika i tehnika Elektronika :: Mikrokontroleri Elektronika :: Audio-elektronika Auto-elektronika :: Tuning Vodič za učenje Vodič za posao Vodič za emigraciju Fizika Matematika Nauka Sertifikati Informatika Vodič za učenje :: Seminarski radovi Vodič za učenje :: Obrazovne institucije Vodič za emigraciju :: Život u USA Vodič za emigraciju :: Život u Norveškoj Vodič za emigraciju :: Život u Nemačkoj E-Poslovanje E-Kupovina IT pravo i politika razvoja IT događaji IT berza poslova IS i ERP Ekonomija Berza Cryptocoins IT berza poslova :: Arhiva IT berze poslova IT pravo i politika razvoja :: Registar Nacionalnog ID E-Poslovanje :: E-Transakcije E-Poslovanje :: Forex E-Kupovina :: Platne kartice Digitalna Televizija Advocacy Ankete Predlozi i pitanja Vesti Čekaonica Vesti :: ES leto manifestacija MadZone TechZone Poljoprivreda AutoZone MotoZone Svakodnevnica Video igre MadZone :: Zanimljivi linkovi MadZone :: Kultura TechZone :: Ergonomija TechZone :: Grejanje TechZone :: Klimatizacija TechZone :: Bela tehnika AutoZone :: Fiat Panda club Lista poslednjih: 16, 32, 64, 128 poruka.

stalker92 Aleksandar (m)ucenik Serbia Član broj: 159503 Poruke: 2 79.101.206.* Profil Aritmeticki nizovi 20.04.2009. u 19:10 - pre 194 meseci Data su dva aritmeticka niza cije su razlike 13 i sqrt(13). Dokazati da postoji najvise jedan broj koji se pojavljuje u oba niza. Treba mi pomoc oko ovog zadatka :( Hvala unapred. BitTorrent je moj prijatelj! Odgovor na temu

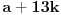
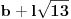
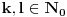
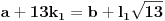
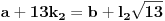
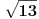
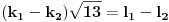
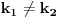
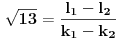
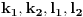
Farenhajt Goran Kapetanović Beograd Član broj: 78132 Poruke: 449 91.148.86.* +6 Profil Re: Aritmeticki nizovi 20.04.2009. u 19:47 - pre 194 meseci Opšti član prvog niza biće , a drugog , gde je . Prepostavimo da postoje dva različita broja koja pripadaju obama nizovima: Oduzimanjem jednačina i skraćivanjem sa dobijamo Po pretpostavci je , što znači da možemo pisati . 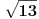Međutim, pošto su nenegativni celi brojevi, to bi značilo da je racionalan broj, a nije. Prema tome, polazna pretpostavka ne valja, te može postojati najviše jedan broj koji se nalazi u oba niza. Napomena: Slučaj gde ne postoji nijedan lako se dobija ako se, recimo, stavi da su i i neki prirodni brojevi. Odgovor na temu

stalker92 Aleksandar (m)ucenik Serbia Član broj: 159503 Poruke: 2 79.101.206.* Profil Re: Aritmeticki nizovi 20.04.2009. u 20:12 - pre 194 meseci Hvala puno!!!! :) BitTorrent je moj prijatelj! Odgovor na temu

cikin ucenik Član broj: 293755 Poruke: 99 *.dynamic.isp.telekom.rs. +1 Profil Re: Aritmeticki nizovi 31.01.2012. u 14:06 - pre 160 meseci da ne stavljam novu temu...postoji li laksi nacin za ovaj, a ne da izvlacim pa izracnunam d, pa a1 pa posle da izracunam zbir,al to mi traje predugo(dobijem tacno resenje)... Četiri broja čine rastući aritmetički niz. Njihov zbir je 16, a zbir njihovih kvadrata 84. Zbir njihovih kubova je?...i za ovaj imam neke ideje al sve su bezuspesne : Niz brojeva b1,b2...b100 je geometrijski. Zbir svih članova niza je pet puta veći od zbira svih članova tog niza sa parnim indeskima. Količnik tog niza je: [Ovu poruku je menjao cikin dana 31.01.2012. u 22:20 GMT+1] Odgovor na temu