Neka je
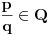
. Iz
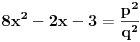
dobijamo
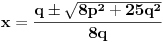
Sada nam ostaje da vidimo kada jednačina
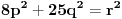
ima cela rešenja (dovoljno je da pronađemo ona kod kojih je
)
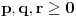
odatle imamo:
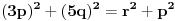
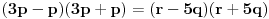
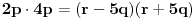
Neka je
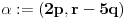
i
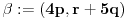
, otuda za neke cele
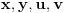
važi:
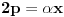
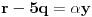
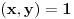
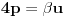
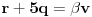
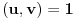
nakon odgovarajućih smena imamo:
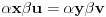
tj.
.
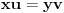
Pošto je
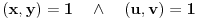
i
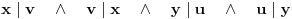
dobijamo dva slučaja:
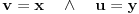
ili
.
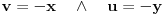
1. slučaj:
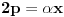
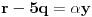
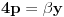
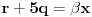
otuda
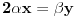
uzmimo da je
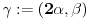
, onda je za neke cele
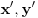
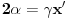
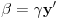
pa dobijamo:
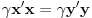
a otuda zbog
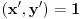
sledi i
i)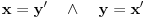 
ii) 
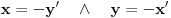
Naravno, dovoljno je da proučimo samo prvi slučaj.
Dakle, imamo
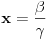
i
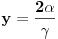
a otuda i:
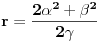
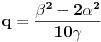
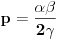
Proverimo da mora biti
:
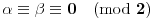
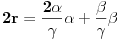
Leva strana je parna, pogledajmo šta se dešava sa parnošću desne u nekoliko slučajeva:
1. Ako je
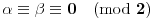
, desna strana (po modulu 2) je
.
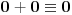
2. Ako je
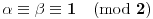
, onda je
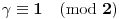
pa je desna strana (po modulu 2)
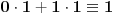3. Ako je
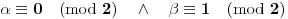
, onda je
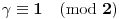
pa je desna strana (po modulu 2)
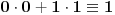4. Ako je
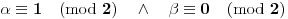
, onda je
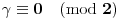
pa je desna strana (po modulu 2)
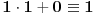
Proverimo da mora biti i
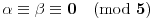
da bi
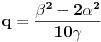
bilo celo.
To možemo videti na sledeći način:
kvadratni ostaci po modulu
su
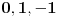
, pa ako bi trebalo da važi
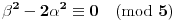
tj.
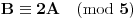
gde su
i
kvadratni ostaci po modulu
- lakom proverom zaključujemo da je jedina mogućnost
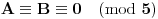
tj.
.
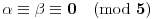
Da zaključimo, ako je
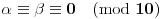
i
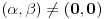
, onda su rešenja:
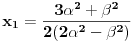
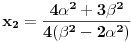
Jasno je da je uvek
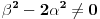
, (osim u trivijalnom slučaju koji smo već isključili)
2. slučaj:
se radi analogno, a rešenja dobijena u tom slučaju već su obuhvaćena rešenjima prvog slučaja.
Ostaje još da se vidi kada je
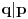
i
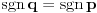
i
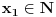
ili
...
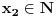
ako baš niko ne bude hteo, onda ću ja malo kasnije 
[Ovu poruku je menjao uranium dana 01.10.2006. u 20:37 GMT+1]
Attempt all the problems. Those you can do, don't do. Do the ones you cannot.
A(x):=sqrt(8x^2 - 2x - 3)
Re: A(x):=sqrt(8x^2 - 2x - 3)
