[es] - Skup R je neprebrojiv!

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dial.InfoSky.Net.

+2801 Profil

^{18.12.2005. u 11:00 - pre 235 meseci}

Ako uspeš da dokažeš da se dijagonalizacijom dobija broj koji je racionalan, izvešćeš kontradikciju iz opšteprihvaćenih matematičkih principa, pa će neki od njih morati da budu odbačeni.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.smin.sezampro.yu.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+621 Profil

Re: Skup R je neprebrojiv!

^{18.12.2005. u 16:20 - pre 235 meseci}

@dust:

Nemam ništa protiv da ovde izneseš kako bi se to moglo dokazati, pa da diskutujemo. Ja, eto, imam utisak da ne može.

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu

dust
Dušan Stefanović

Član broj: 9827
Poruke: 33
*.rcub.bg.ac.yu.

Profil

Re: Skup R je neprebrojiv!

^{18.12.2005. u 22:55 - pre 235 meseci}

Ma meni je taj Kantor malo cudan. Sve je pocelo na logici kad smo radili teoremu koja kaze da postoji prebrojiv skup koji zadovoljava aksiome realnih brojeva (naravno ne kaze koji je to skup). A onda sam malo prelistao Kadelburga i nasao dat Kantorov dokaz, i bas mi je izgledalo kao da je moguce zameniti skup realnih brojeva sa skupom racionalnih. Cisto sam hteo da vidim da li neko jos misli slicno, naravno stoji da broj oblika 0.x1x2... ne mora biti racionalan, ali mi se cini da je moguce dobiti racionalan broj dijagonalnim postupkom. Ocigledno nemam dokaz...

Odgovor na temu

peddja_stankovic
predrag stankovic
private
beograd

Član broj: 48085
Poruke: 221
*.r62.logikom.net.

Sajt: www.geocities.com/predrag..

Profil

Re: Skup R je neprebrojiv!

^{19.12.2005. u 07:09 - pre 235 meseci}

Nemas garanciju da konstruisan broj ima beskonacan periodicni decimalan zapis sto je potrebno (i dovoljno) da broj bude racionalan

tisuću lijepih žena posve nagih

Odgovor na temu

dust
Dušan Stefanović

Član broj: 9827
Poruke: 33
*.120.eunet.yu.

Profil

Re: Skup R je neprebrojiv!

^{19.12.2005. u 17:19 - pre 235 meseci}

Zaboravio sam da se ogradim, kada sam rekao Kantorov dijagonalni postupak, mislio sam na ono sto je dato u Kadelburgovoj knjizi kao dokaz da je skup realnih brojeva neprebojiv. Posto nisam dublje ulazio u teoriju brojeva i teoriju skupova, moje predznanje je malo labavo.

Nemam trenutno Kadelburgovu knjigu kod sebe, ali koliko se secam, ovako bi otprilike zvucao dokaz kad bismo govorili o prirodnim brojevima.

Neka su jos prirodni brojevi definisani kao klase ekvivalencije, tako da je broj jedan :
1
01
001
00....001 itd.

Sada okrenimo postupak tako da polazimo sa desne strane i uzmimo recimo 10 brojeva.

dakle brojevi su:
0000000001
0000000002
0000000003
0000000004
0000000005
0000000006
0000000007
0000000008
0000000009
0000000010

trazimo broj
x10x9x8x7x6x5x4x3x2x1

x1 moze biti 9
x2 moze biti 9
.
.
.
x10 moze biti 9

i dakle dobijeni broj moze biti 9999999999

Ako se dobro secam tu se dokaz zavrsava i kaze se eto dobijeni broj se razlikuje od svakog broja u nizu pa je dati skup neprebrojiv.

Mozda sam ja nesto prevideo tu, kao sto rekoh imam slabo predznanje iz datih oblasti, ali moj mali mozak nece da prihvati ovakav dokaz.

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.adsl.sezampro.yu.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+621 Profil

Re: Skup R je neprebrojiv!

^{19.12.2005. u 20:15 - pre 235 meseci}

Dust, to što si ti napisao je upravo ono što je napisao peddja_stankovic negde pri početku teme, i o čemu smo uranium i ja razvukli raspravu naširoko i nadugačko. Predlažem ti da to sve pročitaš, zaista ima dosta informacija, i ako ti ni onda ne bude jasno javi se za dodatno pojašnjenje, ali mislim da trenutno nema smisla ponavljati sve još jednom.

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu

dust
Dušan Stefanović

Član broj: 9827
Poruke: 33
*.yurail.co.yu.

Profil

Re: Skup R je neprebrojiv!

^{20.12.2005. u 12:42 - pre 235 meseci}

pa da, samo sto je prebaceno na prirodne brojeve

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.smin.sezampro.yu.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+621 Profil

Re: Skup R je neprebrojiv!

^{20.12.2005. u 12:49 - pre 235 meseci}

Aha, e pa tako ne može jer svaki prirodan broj ima samo konačno mnogo cifara.

Ne može ni za racionalne, jer ako imaš beskonačno mnogo cifara i dalje nemaš garanciju da je broj koji one određuju racionalan, može biti racionalan ili iracionalan i nemaš načina da to saznaš.

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu

Farenhajt
Goran Kapetanović
Beograd

Član broj: 78132
Poruke: 449
62.193.129.*

+6 Profil

Re: Skup R je neprebrojiv!

^{20.12.2005. u 16:35 - pre 235 meseci}

Možda ću nešto i lupiti (zarđao sam, izvinjavam se svima koji su u kondiciji), ali zar Kantorovu dijagonalizaciju ne možeš početi proizvoljno daleko od decimalnog zareza? Tj. ako ustanoviš da su ti pokrivene sve moguće kombinacije prvih 5 decimala - od 0,00000xxxx... do 0,99999xxxx... - počećeš dijagonalizaciju od šeste. Ako ti je iscrpljeno prvih milijardu decimala (ili decimale od milionite do milijardite), počećeš od milijardu prve, itd. Pri tome ne možeš kao kontraprimer koristiti konstrukcije na beskonačnim domenima - recimo "a šta ću ako su mi iscrpljene sve decimalne pozicije s parnim indeksom?" - jer prethodno moraš dokazati da se brojevi oblika 0,0x0y0z0t0w... zaista mogu poređati u spisak, tj. da je njihov skup prebrojiv, a to važi akko je prebrojiv skup brojeva oblika 0,xyztw... - dakle, polazni skup.

Dakle, Kantorovoj dijagonalizaciji "opiraće se" konačno mnogo brojeva, što neće uticati na njen rezultat.

Sem toga, uranium je svojevremeno napisao:

Citat:

Zamerka je u tome što je konstrukcija kojom se generiše broj

ostvariva akko broj

nije na spisku, a to je baš ono što se i htelo dokazati...

Ovde se implicira da je broj

jednoznačno određen. Međutim, za svaku cifru "Kantorovog dijagonalnog broja" može se uzeti bilo koja od 9 preostalih cifara (tj. 9 cifara različitih od

), te uraniumu sleduje da dokaže da takvih brojeva (dakle, kandidata za "Kantorov dijagonalni broj") može biti najviše prebrojivo mnogo, posle čega bi s pravom mogao tvrditi da procedura može upasti u ćorsokak. Međutim, mislim da u dokazivanju toga neće uspeti.

_{[Ovu poruku je menjao Farenhajt dana 20.12.2005. u 18:02 GMT+1]}

Odgovor na temu

dust
Dušan Stefanović

Član broj: 9827
Poruke: 33
212.62.59.*

Profil

Re: Skup R je neprebrojiv!

^{21.12.2005. u 11:17 - pre 235 meseci}

Citat:

Bojan Basic: Aha, e pa tako ne može jer svaki prirodan broj ima samo konačno mnogo cifara.

Otkud to?

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.smin.sezampro.yu.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+621 Profil

Re: Skup R je neprebrojiv!

^{21.12.2005. u 11:54 - pre 235 meseci}

Otkud šta? Svaki prirodan broj ima 100, 1000, 1000000, 1000000000 ili koliko hoćeš cifara, ali ne može da ima beskonačno mnogo.

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu

peddja_stankovic
predrag stankovic
private
beograd

Član broj: 48085
Poruke: 221
*.r62.logikom.net.

Sajt: www.geocities.com/predrag..

Profil

Re: Skup R je neprebrojiv!

^{23.12.2005. u 22:48 - pre 235 meseci}

Nesto mi je palo na pamet i mislim da bi ovo moglo da bude znacajno.

Krenucu sa pitanjem prvo.
Uzmimo prvo 1
zatim 2 i 3,
pa onda 4, 5, 6, 7,
pa onda 8, 9, 10, 11, 12, 13, 14, 15,
itd, itd.

Dakle uzeo sam
2⁰ brojeva zatim
2¹ brojeva zatim
2² brojeva zatim
2³ brojeva itd itd.

Nastavimo taj proces u beskraj.

Pitanje: Da li ce mi za taj postupak biti dovoljno prirodnih brojeva?

Ako je odgovor NE, tada pada popularan dokaz da je harmonijski red divergentan
Ako je odgovor DA moglo bi se pokazati da je (0,1) prebrojiv.
I treca opcija negde gresim ili nesto ne znam?

_{[Ovu poruku je menjao peddja_stankovic dana 23.12.2005. u 23:50 GMT+1]}

_{[Ovu poruku je menjao peddja_stankovic dana 24.12.2005. u 00:15 GMT+1]}

tisuću lijepih žena posve nagih

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.dialup.neobee.net.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+621 Profil

Re: Skup R je neprebrojiv!

^{23.12.2005. u 23:53 - pre 235 meseci}

Citat:

peddja_stankovic:
Pitanje: Da li ce mi za taj postupak biti dovoljno prirodnih brojeva?

Ne razumem u kom smislu "dovoljno". Ukoliko je pitanje da li ćemo moći da uzimamo beskonačno mnogo tura, onda je odgovor da.

Citat:

peddja_stankovic:
Ako je odgovor DA moglo bi se pokazati da je (0,1) prebrojiv.

Ipak ne vidim kako bi ovo moglo da se pokaže. Može li malo pojašnjenje ideje?

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu

peddja_stankovic
predrag stankovic
private
beograd

Član broj: 48085
Poruke: 221
*.r62.logikom.net.

Sajt: www.geocities.com/predrag..

Profil

Re: Skup R je neprebrojiv!

^{24.12.2005. u 02:42 - pre 235 meseci}

Uzmimo binarni zapis brojeva od 0 do 1.

0.0110110110001010110011010101010101001010111100101.....

je neki broj iz (0,1).

Obratimo paznju samo na dva broja:

0.0 i
0.1

Sada obratimo paznju na

0.00
0.01
0.10
0.11

Ima ih 4.

Sada na

0.000
0.001
0.010
0.011
0.100
0.101
0.110
0.111

Ima ih 8

itd itd.

Ponavljajuci ovaj postupak u beskraj dobicemo sve varijacije sa ponavljanjem sa beskonacno mnogo cifara. Njih ima 2+4+8+16+.... , upravo koliko i brojeva iz moje prethodne poruke. Znaci mozemo prebrojati sve realne brojeve iz (0,1).

U literaturi i pise da continuum = 2^alef0 gde je alef0 "broj" prirodnih brojeva.

tisuću lijepih žena posve nagih

Odgovor na temu

uranium
Beograd

Član broj: 60097
Poruke: 543
*.eunet.yu.

Jabber: uranium@elitesecurity.org
ICQ: 324386953

+5 Profil

Re: Skup R je neprebrojiv!

^{24.12.2005. u 07:31 - pre 235 meseci}

Ovim postupkom je prebrojan samo jedan podskup racionalnih brojeva iz intervala

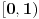
- tj. onih sa konačnim binarnim zapisom. Na primer, ni jedan racionalan broj oblika

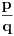
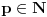
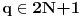
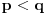
neće biti "uhvaćen" ovim postupkom.

Sledeća primedba nije upućena Peđi.

Što se tiče zapisa

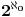
treba imati u vidu:

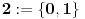
oznaka

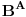
je oznaka za skup svih preslikavanja iz

ako prihvatimo aksiomu izbora, onda je

.

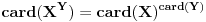
A motivaciju bi trebalo tražiti u sledećem:

Svakom binarnom zapisu realnog broja iz intervala

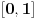
možemo pridružiti karakterističnu funkciju nekog podskupa

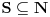
. Naravno, ovde su mogući i ekvivalentni zapisi ( npr.

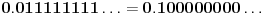
) a problemi koje to izaziva lako se mogu prevazići, jer takvih brojeva (tj. odgovarajućih podskupova) ima samo prebrojivo mnogo, pa njihovo uklanjanje ne menja kardinalnost skupa

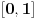
(odnosno skupa

).

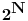
Dakle, izgleda da je kombinatorika na beskonačnim skupovima - vrlo nezgodna (ali i uzbudljiva) disciplina

_{[Ovu poruku je menjao uranium dana 24.12.2005. u 09:36 GMT+1]}

_{Attempt all the problems. Those you can do, don't do. Do the ones you cannot.}

Odgovor na temu

uranium
Beograd

Član broj: 60097
Poruke: 543
*.eunet.yu.

Jabber: uranium@elitesecurity.org
ICQ: 324386953

+5 Profil

Re: Skup R je neprebrojiv!

^{24.12.2005. u 09:07 - pre 235 meseci}

Tek sad sam primetio da je poruka koju je poslao Farenhajt bila menjana.

Citat:

Farenhajt: Ovde se implicira da je broj

jednoznačno određen. Međutim, za svaku cifru "Kantorovog dijagonalnog broja" može se uzeti bilo koja od 9 preostalih cifara (tj. 9 cifara različitih od

Čak i kad se ograničimo na izbor samo dve cifre (

) dobijamo da je

, (svakom broju iz

odgovara jedan binaran zapis broja iz

) dakle sve i da hoću, zaista nema šanse da dokažem da je skup kandidata najviše prebrojiv a da to ne bude kao u ovoj šali:
"There is no logical foundation of mathematics, and Gödel has proved it!"

_{Attempt all the problems. Those you can do, don't do. Do the ones you cannot.}

Odgovor na temu

peddja_stankovic
predrag stankovic
private
beograd

Član broj: 48085
Poruke: 221
*.r62.logikom.net.

Sajt: www.geocities.com/predrag..

Profil

Re: Skup R je neprebrojiv!

^{24.12.2005. u 18:11 - pre 235 meseci}

Cim sam poslao ideju posumljao sam da sam ustvari dokazivao broj racionalnih brojeva. Ipak verujem da se tu moze mnogo toga iscackati. Pa zato "natrag u laboratoriju" kao sto rece Pera Kojot Super Genije.

tisuću lijepih žena posve nagih

Odgovor na temu

Bojan Basic
Novi Sad

SuperModerator
Član broj: 6578
Poruke: 3996
*.dialup.neobee.net.

Jabber: bojan_basic@elitesecurity.org
ICQ: 305820253

+621 Profil

Re: Skup R je neprebrojiv!

^{24.12.2005. u 18:40 - pre 235 meseci}

Kao što reče uranium, nisu čak ni racionalni brojevi nego samo neki od njih - u postupku nije uhvaćen nijedan broj sa beskonačno mnogo binarnih decimala.

Lično, ne verujem da se može mnogo toga iščačkati jer bi to značilo da istovremeno možemo dokazati neko tvrđenje i njegovu negaciju, a iz toga bi sledilo da aksiome koje su u upotrebi nizu konzistentne, i samim tim pada skoro celokupna dosadašnja matematika - strašno, nije li? :)

Ipak, u svakom slučaju sam raspoložen da pročitam nove ideje pa možemo diskutovati i o njima.

Ljubičice crvena, što si plava kô zelena trava.

Odgovor na temu

Nedeljko
Nedeljko Stefanović

Član broj: 314
Poruke: 8704
*.dial.InfoSky.Net.

+2801 Profil

Re: Skup R je neprebrojiv!

^{24.12.2005. u 19:48 - pre 235 meseci}

Citat:

uranium: ako prihvatimo aksiomu izbora, onda je

Koliko znam, to je definicija stepenovanja kardinala. Definicije se ne dokazuju, pa samim tim ne zahtevaju nikakve aksiome, pa ni aksiomu izbora.

Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.

Odgovor na temu