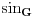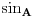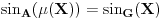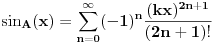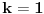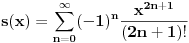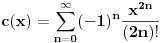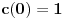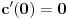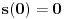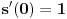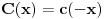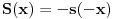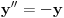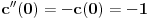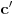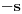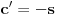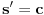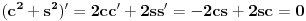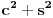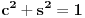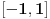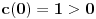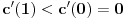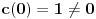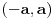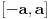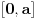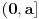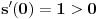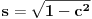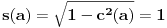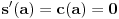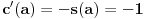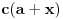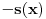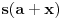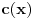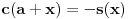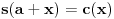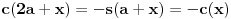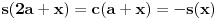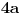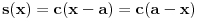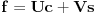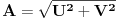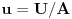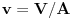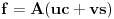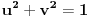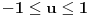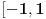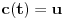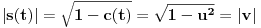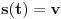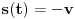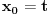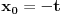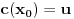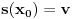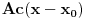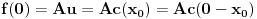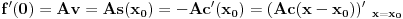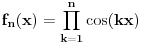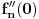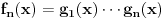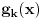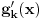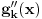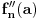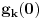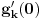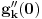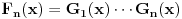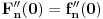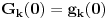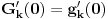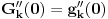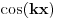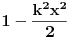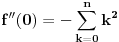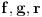 kao u zadatku, pri čemu je
kao u zadatku, pri čemu je 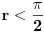 i izvedimo protivrečnost.
i izvedimo protivrečnost.Teorema 1: Neka su
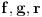 kao u zadatku. Tada je
kao u zadatku. Tada je 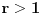 .
.Dokaz: Iz neprekidnosti funkcije
 na ograničenom zatvorenom intervalu
na ograničenom zatvorenom intervalu 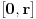 sledi da funkcija
sledi da funkcija  na tom intervalu dostiže najveću vrednost
na tom intervalu dostiže najveću vrednost  u nekoj tački
u nekoj tački  . Iz
. Iz 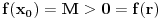 sledi da je
sledi da je 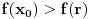 , a samim tim i
, a samim tim i 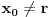 , odnosno
, odnosno 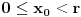 . Za neko
. Za neko 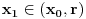 važi sledeće:
važi sledeće: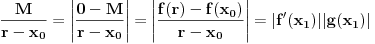 ,
,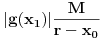 ,
,Za neko
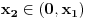 važi sledeće:
važi sledeće: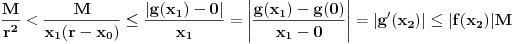 ,
,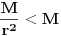 ,
,što zajedno sa
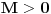 daje
daje 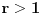 .
.Kraj dokaza.
Teorema 2: Neka su
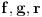 kao u zadatku. Tada postoji
kao u zadatku. Tada postoji 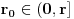 , kao i neprekidne funkcije
, kao i neprekidne funkcije 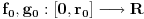 diferencijabilne na intervalu
diferencijabilne na intervalu 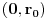 takve da važi
takve da važi 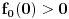 ,
, 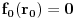 ,
, 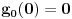 ,
, 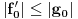 ,
, 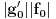 , kao i
, kao i 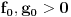 na
na 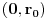 .
.Dokaz: Iz neprekidnosti funkcije
 na ograničenom, zatvorenom intervalu
na ograničenom, zatvorenom intervalu 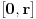 i
i 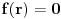 sledi da postoji najmanja nula
sledi da postoji najmanja nula 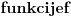 na intervalu
na intervalu 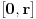 . Pritom, iz
. Pritom, iz 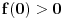 sledi da je
sledi da je 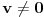 , a samim tim i
, a samim tim i 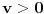 . Dakle,
. Dakle,  je različito od nule na intervalu
je različito od nule na intervalu 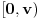 na zbog neprekidnosti na njemu ne menja znak, pa iz
na zbog neprekidnosti na njemu ne menja znak, pa iz 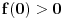 sledi da je
sledi da je 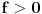 na intervalu
na intervalu 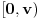 .
.Iz Teoreme 1 sledi da je
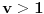 . Dokažimo da funkcija
. Dokažimo da funkcija  nema nula na intervalu
nema nula na intervalu 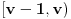 . Dokaz izvodimo svođenjem na protivrečnost. Pretpostavimo da je
. Dokaz izvodimo svođenjem na protivrečnost. Pretpostavimo da je 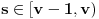 nula funkcije
nula funkcije  i izvedimo protivrečnost. Tada bi za funkcije
i izvedimo protivrečnost. Tada bi za funkcije 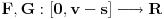 definisane sa
definisane sa 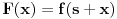 i
i 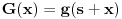 važilo da su neprekidne na
važilo da su neprekidne na 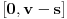 , diferencijabilne na
, diferencijabilne na 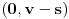 , kao i
, kao i 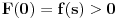 ,
, 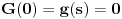 ,
, 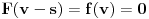 ,
, 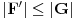 i
i 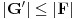 , pa prema Teoremi 1 važi
, pa prema Teoremi 1 važi 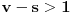 suprotno izboru broja
suprotno izboru broja  .
.Iz neprekidnosti funkcije
 na ograničenom i zatvorenom intervalu
na ograničenom i zatvorenom intervalu 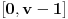 i
i 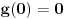 sledi da funkcija
sledi da funkcija  ima najveću nulu
ima najveću nulu  na intervalu
na intervalu 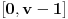 . Pošto funkcija
. Pošto funkcija  nema nula na intervalu
nema nula na intervalu 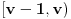 , zaključujemo da je
, zaključujemo da je 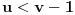 i da je
i da je  najveća nula funkcije
najveća nula funkcije  na intervalu
na intervalu 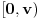 . Dakle, funkcija
. Dakle, funkcija  nema nula na intervalu
nema nula na intervalu 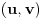 , pa na njemu ne menja znak, pa važi jedno od sledećeg:
, pa na njemu ne menja znak, pa važi jedno od sledećeg:a)
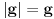 na
na 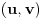 ,
,b)
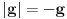 na
na 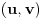 .
.Iz neprekidnosti funkcija
 ,
, 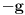 i
i 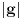 zaključujemo da ista jednakost važi i na intervalu
zaključujemo da ista jednakost važi i na intervalu 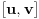 .
.Sada se lako zaključuje da su traženi uslovi ispunjeni za
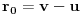 ,
, 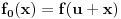 i
i 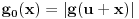 .
.Kraj dokaza.
Dokažimo napokon da je
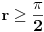 . Pretpostavimo suprotno i izvedimo protivrečnost. Prema Teoremi 2 možemo bez umanjenja opštosti pretpostaviti da je
. Pretpostavimo suprotno i izvedimo protivrečnost. Prema Teoremi 2 možemo bez umanjenja opštosti pretpostaviti da je 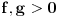 na
na 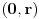 . Definišimo funkciju
. Definišimo funkciju 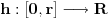 na sledeći način:
na sledeći način: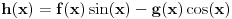 .
.Važi sledeće:
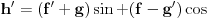 .
.Iz
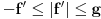 sledi da je
sledi da je 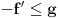 , odnosno
, odnosno 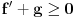 . Iz
. Iz 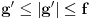 sledi da je
sledi da je 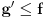 odnosno
odnosno 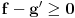 . Odatle i iz
. Odatle i iz 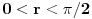 sledi da je
sledi da je 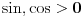 na intervalu
na intervalu 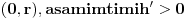 na
na 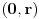 . Odatle i iz neprekidnosti funkcije
. Odatle i iz neprekidnosti funkcije 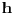 na
na 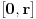 sledi da je funkcija
sledi da je funkcija 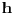 monotono neopadajuća na
monotono neopadajuća na 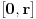 .
.Odatle i iz
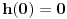 i
i 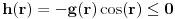 sledi da je funkcija
sledi da je funkcija 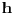 konstantno jednaka nuli, odnosno da je
konstantno jednaka nuli, odnosno da je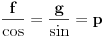 na
na 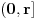 za neku funkciju
za neku funkciju  koja je neprekidna na
koja je neprekidna na 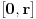 i diferencijabilna i pozitivna na
i diferencijabilna i pozitivna na 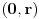 . Drugim rečima, važi
. Drugim rečima, važi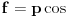 ,
, 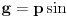 .
.Iz
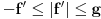 sledi da je
sledi da je 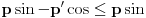 , odnosno
, odnosno 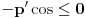 , odnosno
, odnosno 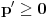 .
.Iz
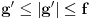 sledi da je
sledi da je 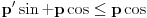 , odnosno
, odnosno 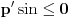 , odnosno
, odnosno 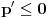 .
.Dakle,
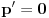 na
na 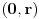 , pa je neprekidna funkcija
, pa je neprekidna funkcija  konstantna na
konstantna na 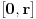 . Pritom je
. Pritom je 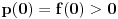 , pa za pozitivnu konstantu
, pa za pozitivnu konstantu  važi
važi 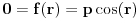 , odnosno
, odnosno 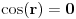 što je u suprotnosti sa pretpostavkom da je
što je u suprotnosti sa pretpostavkom da je 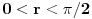 .
.



 Re: Najmanje pozitivno realno r
Re: Najmanje pozitivno realno r