Citat:
miki069: Zadatak je da se izegenerišu sve tetive, a ne samo da se pokrije cela površina kruga.
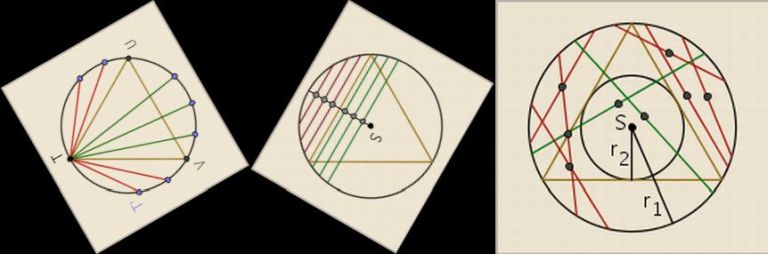
Ali on jeste izgenerisao sve tetive, to što je na ilustraciji samo jedan primer, sa samo jednom, ili dve tačke, u zavisnosti od metoda, važi i za sve ostale slučajeve slučajnog biranja tačke na kružnici ili unutar .. kao na slici ..
Citat:
Fizički model bi bio bacanje štapa na krug, pa merenje dužine tetive.
To već ima kod njega, on je to ilustrovao kao "bacanje slamčice na krug", a rezultat takvog eksperimenta je uvek 1/2
Citat:
Napisao sam programče koje random gađa dve tačke u krugu, pa jednačina prave kroz te dve tačke i onda presek sa kružnicom, pa dužina tetive.
Verovatnoća kovergira ka 21.7%. Zbunjuje me rezultat od 21.7%.
Ha! A mene izgleda ne, u stvari tvoj rezultat je 1/5 nastavak progresije koju je on našao, onih 1,7% viška je bag softvera koji glumi random generator slučajnih brojeva. A evo i kako i zašto izgleda, njegova progresija je biranje jedne tačke na kružnici - rezultat 1/2, dve tačke na kružnici - rezultat 1/3, jedna tačka unutar kružnice - rezultat 1/4, ... ti si se odlučio za biranje dve tačke unutar kružnice, rezultat je 1/5 ... čak sam smislio i fizički eksperiment koji će da pokaže naočigled da si bespogovorno u pravu .. ti bi mogao da bacaš na tablu za pikado onu špaknu za prevrtanje roštilj mesa i šnicli, zašto .. pa zato što ima dva šiljka koji će da simuliraju biranje dve tačke unutar kružnice, zašto se verovatnoća prividno redukuje na 1/5 pa zato što zahvaljući djoki_I i ostalim ljubiteljima roštilj mesa svi znamo da strelica za pikado ima tendenciju baš da pogodi pravo na liniju između 2 broja, i onda se igrači posvađaju i prekine turnir, pa su onda izmislili onu tablu sa metalnom rešetkom baš preko linija, pa onu drugu sa rupicama predviđenim za strelice i elektronskim brojanjem itd .. mislim da se verovatnoća redukuje pri svakom sledećem koraku, matematički, i prividno fizički, zato što se odbacuju svi rezultati gde je 1. slamčica pala tako da dotiče liniju kruga 2. obe skazaljke se poklopile pa dobio jednu tačku 3. pikado pogodio baš na liniju, bilo spoljnu kruga, bilo unutrašnjeg kruga koji služi za određivanje da li je tetiva duža ili ne ... u tvom slučaju tetiva je duža ako je bar jedan šiljak unutar unutrašnjeg kruga, ili ako su oba unutar, a kraća ako su oba u spoljnjem krugu, a odbacivali bi se svi rezultati kad je viljuška pogodila bar jednim šiljkom, ili sa oba, spoljašnji krug, ili unutrašnju kružnicu ... sve te situacije se u fizičkom eksperimentu ne broje, a viljuška dobro pokazuje verovatnoću 1/5.
Slika je ilustracija da se odlučio za biranje jedne tačke na kružnici, dve tačke na kružnici, i jednu tačku unutar kružnice .. ti si se odlučio za dve tačke unutar kružnice.

Način na koji špakna bira dve tačke ...
Citat:
Idealno bi bilo da biram tačke na kružnici, ali je Đoka objasnio da verovatnoća da odabrana tačka bude na kružnici je nula.
Ma kakav djoka on loše objašnjava, naravno da može da bude tačka na kružnici još od prva dva primera dve skazaljke, i slamčice ... još malo da objasnimo i da nas upisuju u panteon matematike ..
Citat:
Mislim da je i izbor 2 tačke u krugu verna simulacija slučajne tetive.
Naravno, ali i sve prethodne su, biranje jedne i dve tačke na kružnici, i biranje jedne tačke unutar kružnice i proglašavanje nje za sredinu tetive ...
Citat:
U datom rešenju nedostaje uslov abs(y-x)<4*pi/3. Sa tim uslovom verovatnoća se menja u 33.33%.
E sad se ja nerviram što ne umem da objasnim jer sam se pogubio u ovim abs, x, y, Pi/3 itd, a dodatno nervira što je rezultat tačno poklapanje sa 1/3 tj. 33,33%, pa onih 1,7% viška ili greške kod biranja dve tačke verovatno potiče od toga što je tvoja softverska "viljuška" varijabilna, čas je uža čas šira u zavisnosti od dve odabrane tačke ... trebalo bi da se smisli grafičko, geometrijsko rešenje gde se krug gađa sa kratkim dužima, i ista takva interpretacija bilo sa rotiranjem unutrašnjeg trougla, bilo sa onom unutrašnjom kružnicom i površinama ... Ah da propustio sam da prebrojim situaciju kad je viljuška pala jako blizu linije unutrašnje kružnice a izvan nje, ali tako da su oba šiljka toliko blizu da tetiva provučena kroz njih prolazi kroz unutrašnju kružnicu, viljuška je izvan, ali je tetiva duža od stranice trougla! Tu se krije onih 1,7% viška!
Nemoj da pricas?