• Naslovna
• FAQ
• Pravilnik
• O ES-u
• Tim
• Korisnici
• Statistike

 

• elitesecurity ::
• elitemadzone ::
• EMAIL ::
• RSS ::
• ES Mobile

  Niste ulogovani?  Username :   Password:   

• Registracija
• Zaboravili ste password?
• Flashback ▲▼
• Login problem?

 

Pretraga:

 

Srodne teme 21.06.2006. Mjurheadova teorema 25.09.2005. Dokaz Pitagorine teoreme ? 14.03.2004. Periodičnost funkcije - elegantan dokaz? 14.08.2004. Pomoc oko jednog limesa 29.12.2004. trigonometrija,Gdje grijesim? 15.09.2005. Odredjivane osnovnog perioda i amplitude funkcije 16.11.2005. Zadatak iz limesa niza 31.03.2009. dokaz ekvivalentnosti definicija limesa po Cauchy.. 16.04.2006. Kratak zadatak iz Limesa 20.11.2006. Dokaz fundamentalne teoreme algebre Navigacija Brisanje liste Aktuelne teme u ovom forumu: Još jedan zadatak sa uglovima Treći zadatak sa uglovima Ostala rešenja algebarske jednačine Lep zadatak sa uglovima Najmanje pozitivno realno r Ikosaedar i gustina ms matematika.... Jedan zadatak sa pravouglim trouglom Japanese | Can you solve this ? | Math.. Jednakostraničan trougao Logaritamska nejednakost Raspoređivanje slova Košarkaši lep zadatak Zanimljiv zadatak o uglovima trougla Stado Boga Sunca ... 2000 godina star .. Izaberite forum: Linux Linux aplikacije Linux desktop okruženja Linux hardware Windows desktop Windows aplikacije Zaštita Office Windows drajveri Office :: Word Office :: Excel Macintosh Mac hardware Mac software Iphone Enterprise Networking SOHO Networking Wireless Windows mreže Linux mreže Wireless :: WiMax Wireless :: Mikrotik Wireless :: Wireless oprema Linux/UNIX serveri i servisi Unix BSD Skript jezici Security Virtualizacija Cloud Computing Services Security :: Kriptografija i enkripcija .NET 3D programiranje Art of Programming Asembler C/C++ programiranje Kernel i OS programiranje Pascal / Delphi / Kylix Java Embedded sistemi Perl PHP Python Visual Basic 6 Veštačka inteligencija Security Coding XML GameDev - Razvoj Igara Ostali programski jezici PHP :: PHP za početnike PHP :: Smarty template engine .NET :: .NET Desktop razvoj .NET :: ASP.NET .NET :: WPF Programiranje C/C++ programiranje :: C/C++ za početnike Baze podataka MySQL Oracle Access MS SQL Firebird/Interbase PostgreSQL Fiksna telefonija VoIP Udruženje korisnika teleko.. GSM - telefoni GSM - upotreba GSM - servisiranje Mreže i novosti Smartphone Mreže i novosti :: Mobilni internet Mreže i novosti :: Telenor - korisnički servis Mreže i novosti :: VIP - korisnički servis Mreže i novosti :: MTS - korisnički servis Smartphone :: Symbian OS Smartphone :: Windows Mobile Smartphone :: Android GSM - telefoni :: Nokia PDA Uređaji GPS Portable Players Anonimnost i privatnost ISP Browseri E-mail Instant Messaging FTP Google Hosting ISP :: Wireless mreže i ISP ISP :: ADSL E-mail :: Anti-spam Instant Messaging :: IRC Hosting :: Domeni Google :: Gmail E-Marketing Web aplikacije Web dizajn i CSS Web dizajn softver Web razvoj Pretraživači i SEO Flash Javascript i AJAX Web dizajn i CSS :: Kritike Grafički dizajn Izdavaštvo 3D modelovanje Rasterska grafika Vektorska grafika 3D modelovanje :: CAD/CAM Matične ploče, procesori .. Video karte i monitori Storage Ostali hardver Overclocking & Modding PC Konfiguracije Laptopovi Vodič za kupovinu - PC har.. Tablet PC Muzička produkcija Audio kompresija Audio softver Video produkcija Video kompresija Video softver Multimedijalni uređaji Digitalni fotoaparati Digitalne kamere Home Theater Digitalni fotoaparati :: Fotografija Digitalni fotoaparati :: Vodič za kupovinu - Digita.. Elektronika Elektrotehnika Elektronika :: TV uređaji Elektronika :: Radio elektronika i tehnika Elektronika :: Mikrokontroleri Elektronika :: Audio-elektronika Auto-elektronika :: Tuning Vodič za učenje Vodič za posao Vodič za emigraciju Fizika Matematika Nauka Sertifikati Informatika Vodič za učenje :: Seminarski radovi Vodič za učenje :: Obrazovne institucije Vodič za emigraciju :: Život u USA Vodič za emigraciju :: Život u Norveškoj Vodič za emigraciju :: Život u Nemačkoj E-Poslovanje E-Kupovina IT pravo i politika razvoja IT događaji IT berza poslova IS i ERP Ekonomija Berza Cryptocoins IT berza poslova :: Arhiva IT berze poslova IT pravo i politika razvoja :: Registar Nacionalnog ID E-Poslovanje :: E-Transakcije E-Poslovanje :: Forex E-Kupovina :: Platne kartice Digitalna Televizija Advocacy Ankete Predlozi i pitanja Vesti Čekaonica Vesti :: ES leto manifestacija MadZone TechZone Poljoprivreda AutoZone MotoZone Svakodnevnica Video igre MadZone :: Zanimljivi linkovi MadZone :: Kultura TechZone :: Ergonomija TechZone :: Grejanje TechZone :: Klimatizacija TechZone :: Bela tehnika AutoZone :: Fiat Panda club Lista poslednjih: 16, 32, 64, 128 poruka.

miki069 Član broj: 161528 Poruke: 2056 *.dynamic.mbb.telenor.rs. +390 Profil Re: Dokaz teoreme tablicnog limesa? - (sinx/x) 02.05.2023. u 06:30 - pre 23 meseci Nizom ekvivalencija je dokazano: (f(c)-f(a))/(c-a) < (f(b)-f(a))/(b-a) To ne znači da je f(x)/x rastuća funkcija. Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 *.dynamic.isp.telekom.rs. +2801 Profil Re: Dokaz teoreme tablicnog limesa? - (sinx/x) 02.05.2023. u 07:42 - pre 23 meseci Nego šta znači za i ? Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 *.dynamic.isp.telekom.rs. +2801 Profil Re: Dokaz teoreme tablicnog limesa? - (sinx/x) 02.05.2023. u 08:38 - pre 23 meseci @BrutalCoin Dakle, iz nejednakosti sledi da za svako važi . Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

miki069 Član broj: 161528 Poruke: 2056 *.mbb.telenor.rs. +390 Profil Re: Dokaz teoreme tablicnog limesa? - (sinx/x) 02.05.2023. u 08:45 - pre 23 meseci Za a=0 i ako je f(0)=0, znači da je rastuća. Za neko drugo a ne znači ništa. Ako f(0) nije nula, takođe ne znači ništa. Pošto je tg(0)=0, može se primeniti. Kada smo dokazali da traženi limes postoji, kako dokazujemo da je = 1? [Ovu poruku je menjao miki069 dana 02.05.2023. u 09:56 GMT+1] Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 *.dynamic.isp.telekom.rs. +2801 Profil Re: Dokaz teoreme tablicnog limesa? - (sinx/x) 02.05.2023. u 17:14 - pre 23 meseci , pa iz konkavnosti funkcije i konveksnosti funkcije sledi da je opadajuća, a rastuća funkcija. Monotone funkcije imaju limes u nuli sa desne strane. Pokazao sam kako se izvodi da je taj limes pozitivan i konačan. Ako uglove meriš u stepenima, a ne u radijanima, onda taj limes nije jednak 1. Međutim, moguć je izbor funkcije mere ugla (koja je određena jednoznačno do na multiplikativnu konstantu), tako da taj limes bude jednak jedinici. Za takav izbor funkcije mere ugla važi da je i , pa je brzina tačke konstantno jednaka jedinici, odakle sledi da je ta funkcija mere ugla jednaka meri ugla u radijanima. Edit: promenjeno u . [Ovu poruku je menjao Nedeljko dana 02.05.2023. u 21:36 GMT+1] Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

BrutalCoin Član broj: 337807 Poruke: 126 +103 Profil Re: Dokaz teoreme tablicnog limesa? - (sinx/x) 03.05.2023. u 05:07 - pre 23 meseci Svi prethodni navedeni metodi dokazivanja "padaju u vodu" jer se pozivaju na izvod sin' = cos. Ti sad napišeš da važi (sin(x))' = cos(x) Šta je onda u tvom izvodjenju dokaza novo kad smo i za (sada već klasičan) geometrijski metod polazili od te iste pretpostavke ((sin(x))' = cos(x)) a zatim taj metod dokazivanja odbacivali upravo zbog te (nedokazane) pretpostavke? Odgovor na temu

miki069 Član broj: 161528 Poruke: 2056 *.mbb.telenor.rs. +390 Profil Re: Dokaz teoreme tablicnog limesa? - (sinx/x) 03.05.2023. u 08:13 - pre 23 meseci Ne poziva se nigde u dokazu na izvod. Kada prihvatimo da je limes = 1, dokazuje da je mera ugla bila u radijanima a ne u stepenima ili gradijanima. Koristi vektor brzine, da bi dokazao radijane. A brzina je prvi izvod radijus vektora. Za mene je dokaz korektan. Još samo da dokažem konveksnost za tg(x). Nije baš trivijalno kao dokaz konkavnosti za sin(x), ali je rešivo. Odgovor na temu

BrutalCoin Član broj: 337807 Poruke: 126 +103 Profil Re: Dokaz teoreme tablicnog limesa? - (sinx/x) 03.05.2023. u 09:13 - pre 23 meseci Citat: Za takav izbor funkcije mere ugla važi da je (sin(x))' = cos(x) i (cos(x))' = -sin(x), pa je brzina tačke konstantno jednaka jedinici Prvo ima izvod "pa" na osnovu toga zaključuje da je brzina konstantno jednaka jedinici. Zar to nije korišćenje izvoda? Mislim, ono, nismo ni morali da potežemo Jensenove nejednakosti nago odmah, du - "imamo takvu meru ugla za koju je brzina konstanto jednaka jedinici!" Onda samo još da odgonetnemo kako smo izabrali baš takvu funkciju? Trial & error? Odgovor na temu

miki069 Član broj: 161528 Poruke: 2056 *.mbb.telenor.rs. +390 Profil Re: Dokaz teoreme tablicnog limesa? - (sinx/x) 03.05.2023. u 10:00 - pre 23 meseci Kada bi ugao x merili u stepenima, onda bi rezultat limesa bio pi/180, a ne 1. Kada bi ugao x merili u gradijanima, onda bi rezultat limesa bio neki treći broj. Ne znam koji, jer ne znam definiciju gradijana. Nedeljko je dokazao da je rezultat limesa konstanta veća od 0 i manja od beskonačnosti. Ako prihvatimo da je limes 1, onda tražimo meru ugla. Može i obrnuto. Mislim da je sve korektno. Odgovor na temu

miki069 Član broj: 161528 Poruke: 2056 *.dynamic.mbb.telenor.rs. +390 Profil Re: Dokaz teoreme tablicnog limesa? - (sinx/x) 03.05.2023. u 13:32 - pre 23 meseci Preko dužine upisanih tetiva. Preko kosinisne teoreme se lako dokaže da je dužina tetive BD jednaka 2*sin(x/2). Ako kružni luk podelimo simetralom ugla x, dobijemo dve upisane tetive čiji je zbir 4*sin(x/4). Posle sledeće podele uglova x/2 simetralama imamo 4 tetive čiji je zbir jednak 8*sin(x/8). Posle n-1 iteracije imamo da je zbir tetiva jednak 2^n*sin(x/(2^n)). Kada pustimo da n teži u beskonačno, intuitivno, zbir tetiva teži dužini kružnog luka x. To jest 2^n*sin(x/(2^n)) teži x. Odatle sin(x/(2^n)) teži ka x/(2^n), što je i dokaz traženog limesa. Prikačeni fajlovi Luk.jpg - 8.58k Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 *.dynamic.isp.telekom.rs. +2801 Profil Re: Dokaz teoreme tablicnog limesa? - (sinx/x) 03.05.2023. u 14:17 - pre 23 meseci Mera ugla se može odabrati tako da važi , a odatle se lako izvode obrasci za izvode sinusa i kosinusa za istu tu meru ugla. Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

miki069 Član broj: 161528 Poruke: 2056 *.mbb.telenor.rs. +390 Profil Re: Dokaz teoreme tablicnog limesa? - (sinx/x) 03.05.2023. u 15:27 - pre 23 meseci Da ne petljam sa simetralama. BD = 2*sin(x/2) < x Da li može da se prihvati da kada x teži nuli da dužina tetive BD teži ka x? Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 *.dynamic.isp.telekom.rs. +2801 Profil Re: Dokaz teoreme tablicnog limesa? - (sinx/x) 03.05.2023. u 19:56 - pre 23 meseci Ne može jer je x promenljiva iz graničnog procesa. Verovatno si mislio da količnik te dve veličine teži jedinici. Opet, to zavisi od izbora funckije mere ugla. Moguć je i pristup sa površinama, ali onda ima drugih stavova koje treba dokazati. Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

BrutalCoin Član broj: 337807 Poruke: 126 +103 Profil Re: Dokaz teoreme tablicnog limesa? - (sinx/x) 04.05.2023. u 10:48 - pre 23 meseci Citat: miki069 Kada bi ugao x merili u stepenima, onda bi rezultat limesa bio pi/180, a ne 1. Sad sam ukapirao... Vi pod "funkcija mere ugla" podrazumevate jedinice mere. Ja to posmatram kao dva različita pojma. Onda u redu (za limes =1). Tada imaš odgovor i na pitanje Citat: Da li može da se prihvati da kada x teži nuli da dužina tetive BD teži ka x? Dužina tetiva nije funkcija mere ugla, jer ako bi dužinu tetiva uzeli za funkciju mere ugla tada za uglove α1 + α2 = α3 može biti M(α1) + M(α2) > M(α3) pa dužina tetiva nije odgovarajuća mera. Odgovor na temu

miki069 Član broj: 161528 Poruke: 2056 *.mbb.telenor.rs. +390 Profil Re: Dokaz teoreme tablicnog limesa? - (sinx/x) 04.05.2023. u 16:35 - pre 23 meseci Nigde ne mogu da nađem stav da je obim pravilnog n-tougla veći od obima u njega upisane kružnice. Dokaz tog stava bi ujedno bio i lagan dokaz ovog limesa. Dokazao sam konveksnost funkcije tg(x) na intervalu [0,π/2). Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 *.dynamic.isp.telekom.rs. +2801 Profil Re: Dokaz teoreme tablicnog limesa? - (sinx/x) 04.05.2023. u 23:37 - pre 23 meseci Za taj pristup preko površina treba dokazati da se mera ugla može definisati kao površina odgovarajućeg kružnog isečka jediničnog poluprečnika. To se dokazuje primenom invarijantnosti mere za izometrije i aditivnosti mere. Uvedena mera je polovina mere u radijanima. Onda se može primeniti metod sa površinama. Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

miki069 Član broj: 161528 Poruke: 2056 *.dynamic.mbb.telenor.rs. +390 Profil Re: Dokaz teoreme tablicnog limesa? - (sinx/x) 22.05.2023. u 08:39 - pre 23 meseci Da ne otvaram novu temu. Kako bi išao dokaz za: Posle dokaza da je funkcija konveksna imamo da je funkcija rastuća. Odgovor na temu

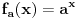
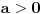
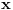
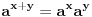
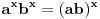
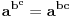
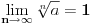
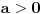
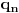
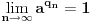
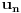
Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 *.dynamic.isp.telekom.rs. +2801 Profil Re: Dokaz teoreme tablicnog limesa? - (sinx/x) 22.05.2023. u 21:18 - pre 23 meseci Prvo uvedi funkciju za i racionalno. Onda dokaži , , i monotoniju i iskoristi za da dokažeš da ako je niz racionalnih brojeva koji teži nuli da je onda . 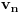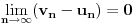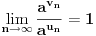To iskoristi da dokažeš sledeće: ako je rastući niz racionalnih brojeva, a opadajući niz racionalnih brojeva, pri čemu je , onda mora biti , odnosno . 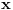To ti omogućava da definišeš jednoznačno za i realno kao jedinstevno neprekidno produženje sa racionalnih eksponenata na realne. 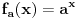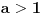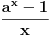Funkcija je za J-konveksna i neprekidna, pa je konveksna, pa je funkcija rastuća. 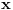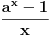Kada sa desne strane teži nuli, onda opada, ali je stalno veće od nule, pa konvergira nenegativnoj vrednosti. 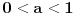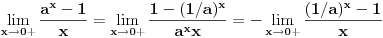Za je , pa se konvergencija svodi na konvergenciju u slučaju da je . 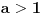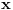Analogno važi i u slučaju kada teži nuli sa leve strane. Pošto smo dokazali konvergenciju, možemo definisati funkciju . 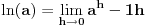Sada se lako izvodi da je . 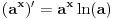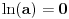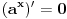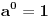Ako je , onda je pa je funkcija konstantna i jednaka vrednosti pa je . 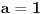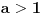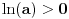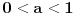Dakle, za je , dok za važi . 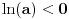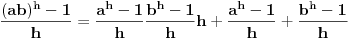Iz identiteta sledi da je . 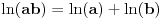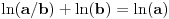Odatle sledi da je , odnosno , . 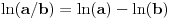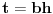Takođe, smenom se dobija da važi . 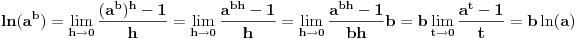Sada je lako izvesti strogu monotoniju funkcije . 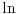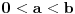Za je . 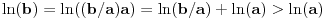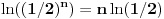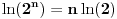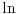Slično, iz i sledi neograničenost funkcije i odozgo i odozdo. Dokažimo neprekidnost. Iz monotonije sledi da postoje limesi i sa leve i sa desne strane. 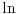Svaka monotona funkcija može imati najviše prebrojivo mnogo tačaka prekida, pa postoje tačke u kojima je funkcija neprekidna. Neka je neprkidna u tački . 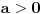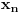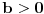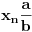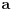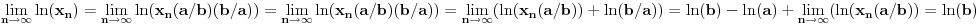Za svaki niz koji konvergira nekoj tački važi da niz konvergira ka , pa važi , pa je neprekidna i u tački . 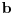Dakle, neprekidna je svuda. 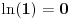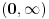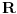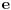Pritom je i sa ob strane neograničena i strogo rastuća, pa je bijekcija skup na , pa postoji jedinstvena vrednost za koju je . 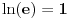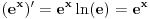Tada važi , a samim tim i . 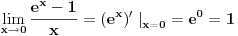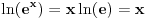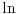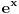Pritom je , pa je ništa drugo do inverzna funkcija funkcije , odnosno logaritam za osnovu . 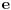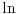Izvod funkcije se sada može izvesti kao izvod inverza funkcije . 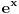Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 *.dynamic.isp.telekom.rs. +2801 Profil Re: Dokaz teoreme tablicnog limesa? - (sinx/x) 23.05.2023. u 07:36 - pre 23 meseci Isparvka, definicija funkcije treba da glasi za . Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

sikira069 Miki Član broj: 348726 Poruke: 22 *.mbb.telenor.rs. +19 Profil Re: Dokaz teoreme tablicnog limesa? - (sinx/x) 18.02.2024. u 21:38 - pre 14 meseci Citat: miki069: Preko dužine upisanih tetiva. Preko kosinisne teoreme se lako dokaže da je dužina tetive BD jednaka 2*sin(x/2). Ako kružni luk podelimo simetralom ugla x, dobijemo dve upisane tetive čiji je zbir 4*sin(x/4). Posle sledeće podele uglova x/2 simetralama imamo 4 tetive čiji je zbir jednak 8*sin(x/8). Posle n-1 iteracije imamo da je zbir tetiva jednak 2^n*sin(x/(2^n)). Kada pustimo da n teži u beskonačno, intuitivno, zbir tetiva teži dužini kružnog luka x. To jest 2^n*sin(x/(2^n)) teži x. Odatle sin(x/(2^n)) teži ka x/(2^n), što je i dokaz traženog limesa. Ako pustimo da n teži u beskonačnost imamo dokaz traženog limesa. Korektno? Odgovor na temu