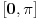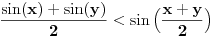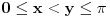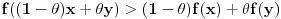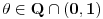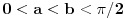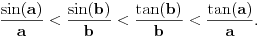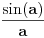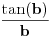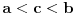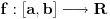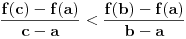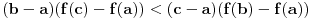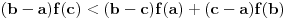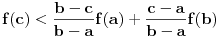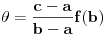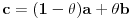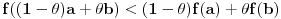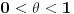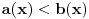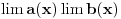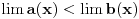Citat:
Nedeljko
BrutalCoin nastupa kao da postoji samo jedan ispravan redosled izlaganja.
Nemoj preterivati. Nisam ja osporio tvoj sistem nego postavljam pitanje kako to uklopiti u postojeći (tj. već uobičajeni) sistem. A postojeći sistem je kako sam napisao "ad-hok" tj. na osnovu iskustva.
A problem x < tg(x) se u praktično celokupnoj literaturi zasniva no onome što su napisli Adnadjević/Kadelburg i oni pre njih. Tj. dokazuje se geometrijski preko površine kružnog isečka.
Nakon dokaza x < tg(x) Adnadjević/Kadelburg dokazuju (na osnovu "dokazanog") da je lim(sinx/x)=1, x-->0.
Zatim navode teoremu o izvodu inverzne funkcije i daju
(arcsinx)' = 1/Sqrt(1-x^2)
pozivajući se na tu teoremu.
E sad je problem lim(sinx/x), x-->0 mada se u pomenutoj teoremi traži lim((f(x)-f(x0))/(x-x0)), x-->x0. A to nije lim(sinx/x), x-->0.
Na primer, Ljaško/Boračuk samo daju lim(sinx/x)=1, X-->0, ali dokaz (trivijalno

) prepuštaju čitaocu i kasnije koriste taj limes za rešavanje zadataka.
U knjizi za elekttrotehnički Mihajlović/Janić takodje koriste geometriju:
Na krugu poluprečnika OA=OB=R sa centralnim uglom AOB=x zaključuju da važi:
area trougla OAB < area sektora OAB < area trougla OAC
area trougla OAB = R^2*sinx/2
area sektora OAB = luk AB*R/2 = R*x*R/2 = R^2x/2
area trougla OAC = OA * OC/2 = R*R*tgx/2 = R^2*tgx/2
Pa dobijaju
R^2*sinx/2 < R^2x/2 < R^2*tgx/2
tj.
sinx < x < tgx ■
Problem, x < tgx, se može rešavati i preko kompleksnih brojeva.
Ali onda za kompleksan broj
z = x + iy
neko može da kaže da je to u stvari
z = r(cosß + isinß), r = |z|
i da sve ospori jer se javlja sinus.
Citat:
Nedeljko:
Može se dokazati da je u desnoj poluokolini nule sinus konkavna, a tangens konveksna funkcija.
Kako dokazuješ da je konveksna? Preko izvoda ili parametarskim putem?
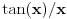 rastuća, a
rastuća, a 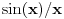 opadajuća, pri čemu važi nejednakost
opadajuća, pri čemu važi nejednakost 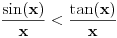 . Odatle se izvodi da traženi limes postoji i da je pozitivan i konačan. Pritom se "može napraviti izbor mernih jedinica" takav da taj limes bude jednak 1.
. Odatle se izvodi da traženi limes postoji i da je pozitivan i konačan. Pritom se "može napraviti izbor mernih jedinica" takav da taj limes bude jednak 1.



 Re: Dokaz teoreme tablicnog limesa? - (sinx/x)
Re: Dokaz teoreme tablicnog limesa? - (sinx/x)