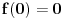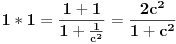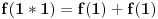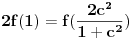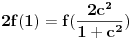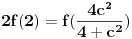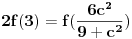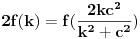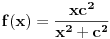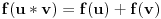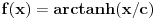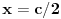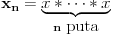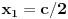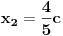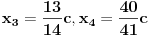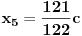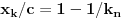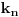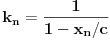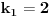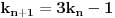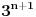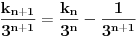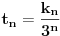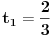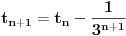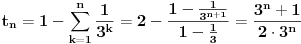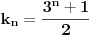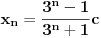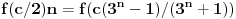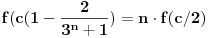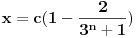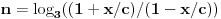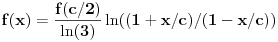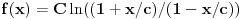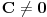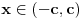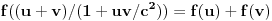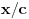Citat:
Nedeljko:
Može li sada neko da dokaže, da za svaku osnovu
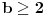
i za svaku ne-nula cifru
sistema sa sonovom
postoji broj koji kada se zapiše u sistemu sa osnovom
, premeštanjem poslednje cifre na prvo mesto se dobija
puta veći broj?
Na isti nacin kako je miki069 prikazao za slucaj
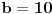
, a istu formulu napisao i number42, moze se dobiti da je trazeni broj jednak
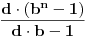
. Dovoljno je pokazati da uvek postoji n takvo da je
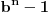
deljivo sa
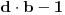
, iako bi naravno moglo da se desi i da
ima zajednicki faktor sa imeniocem. Samo da napomenem da ako se dozvoli da je
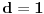
zadatak je trivijalan (resenje je uvek 11, a ako se dozvoli jednocifren broj, onda i 1).
Naravno, uslov ce biti ispunjen ako je
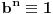
po modulu
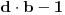
. U opstem slucaju nije prost broj
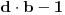
pa umesto Fermaove teoreme, mozemo da koristimo
Ojlerovu. Treba samo pokazati da je
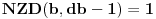
ali to je jednako
.
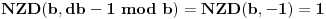
Dakle, to su uvek uzajamno prosti brojevi, pa se primenom Ojlerove teoreme nalazi da je
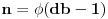
gde je
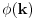Ojlerova funkcija koja predstavlja broj uzajamno prostih brojeva sa k, koji su manji od k. U slucaju da je bd-1 prost broj, kao u prvoj postavci ovog zadatka,
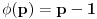
jer su svi brojevi manji od prostog broja p uzajamno prosti za njim.
Re: 13. pitanje..............
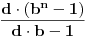
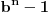
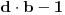
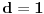
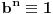
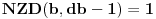
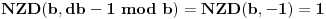
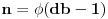
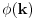
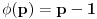
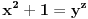
Re: tacno ili netacno: 24 casa
