Rekao sam koji su razlozi zašto se to numerički ne radi.
Ja bih povećavao
počev od 1, pa na gore po n1, sve dok ne nađem da je matrica
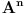
linearna kombinacija matrica
i odredio te koeficijente. To ti je sistem od
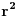
linearnih jednačina po koeficijentima minimalnog polinoma, gde je
red matrice (ne rang, nego je format matrice
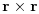
). Korektno rešenje problema imaš samo ukoliko su ti koeficijenti matrice dati tačno, a ne približno i onda bi trebalo koristiti neku biblioteku za rad sa racionalnim brojevima u obliku brojilac/imenilac, pri čemu brojilac i imenilac mogu biti proizvoljno veliki celi brojevi. Jedna od takvih je GMP za C i C++. No, jednostavnije rešenje ti je da koristiš intervalnu algebru iz boost biblioteke, pa da sistem linearnih jednačina rešavaš nekim stabilnim metodom, na primer Gausov metod sa potpunim pivotiranjem, pri čemu ne vršiš delenje nijednim intervalom koji sadrži nulu, jer tu vrednost tretiraš kao nulu. E, onda ako dobiješ da je minimalni polinom nižeg stepena od karakterističnog, to znači da unutar računa te tačnosti ne sledi da je minimalni polinom višeg stepena. Ovo ti je samo uslovno korektno rešenje, a sve zbog činjenica koje sam opisao u prethodnoj poruci.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
Racunanje koeficijenata minimalnog karakteristicnog polinoma
Registrovani: 1 ( vjova )
