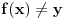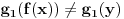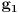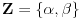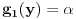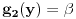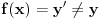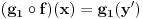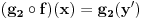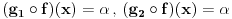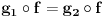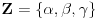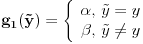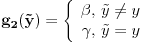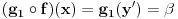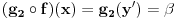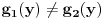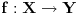• Naslovna
• FAQ
• Pravilnik
• O ES-u
• Tim
• Korisnici
• Statistike

 

• elitesecurity ::
• elitemadzone ::
• EMAIL ::
• RSS ::
• ES Mobile

  Niste ulogovani?  Username :   Password:   

• Registracija
• Zaboravili ste password?
• Flashback ▲▼
• Login problem?

 

Pretraga:

 

Srodne teme 21.01.2004. Zadatak sa opstinskog takmicenja 18.09.2004. funkcija dve promenljive - hesianova matrica 16.06.2005. Dokazivanje poučaka ili poučka. Potrebno 10.09.2005. [zadatak] Iz funkcija 07.10.2005. [Zadatak]: Kompozicija funkcija 02.12.2005. [Zadatak]: Funkcija na pravilnim n-uglima 16.01.2006. zadatak iz graničnih vrednosti funkcija 09.06.2006. Transcedentne funkcije (i brojevi) 12.01.2007. Zadatak - ispitivanje funkcija POMOC !!! 27.04.2007. Zadatak dokazivanje - hitno! Navigacija Brisanje liste Aktuelne teme u ovom forumu: Još jedan zadatak sa uglovima Treći zadatak sa uglovima Ostala rešenja algebarske jednačine Lep zadatak sa uglovima Najmanje pozitivno realno r Ikosaedar i gustina ms matematika.... Jedan zadatak sa pravouglim trouglom Japanese | Can you solve this ? | Math.. Jednakostraničan trougao Logaritamska nejednakost Raspoređivanje slova Košarkaši lep zadatak Zanimljiv zadatak o uglovima trougla Stado Boga Sunca ... 2000 godina star .. Izaberite forum: Linux Linux aplikacije Linux desktop okruženja Linux hardware Windows desktop Windows aplikacije Zaštita Office Windows drajveri Office :: Word Office :: Excel Macintosh Mac hardware Mac software Iphone Enterprise Networking SOHO Networking Wireless Windows mreže Linux mreže Wireless :: WiMax Wireless :: Mikrotik Wireless :: Wireless oprema Linux/UNIX serveri i servisi Unix BSD Skript jezici Security Virtualizacija Cloud Computing Services Security :: Kriptografija i enkripcija .NET 3D programiranje Art of Programming Asembler C/C++ programiranje Kernel i OS programiranje Pascal / Delphi / Kylix Java Embedded sistemi Perl PHP Python Visual Basic 6 Veštačka inteligencija Security Coding XML GameDev - Razvoj Igara Ostali programski jezici PHP :: PHP za početnike PHP :: Smarty template engine .NET :: .NET Desktop razvoj .NET :: ASP.NET .NET :: WPF Programiranje C/C++ programiranje :: C/C++ za početnike Baze podataka MySQL Oracle Access MS SQL Firebird/Interbase PostgreSQL Fiksna telefonija VoIP Udruženje korisnika teleko.. GSM - telefoni GSM - upotreba GSM - servisiranje Mreže i novosti Smartphone Mreže i novosti :: Mobilni internet Mreže i novosti :: Telenor - korisnički servis Mreže i novosti :: VIP - korisnički servis Mreže i novosti :: MTS - korisnički servis Smartphone :: Symbian OS Smartphone :: Windows Mobile Smartphone :: Android GSM - telefoni :: Nokia PDA Uređaji GPS Portable Players Anonimnost i privatnost ISP Browseri E-mail Instant Messaging FTP Google Hosting ISP :: Wireless mreže i ISP ISP :: ADSL E-mail :: Anti-spam Instant Messaging :: IRC Hosting :: Domeni Google :: Gmail E-Marketing Web aplikacije Web dizajn i CSS Web dizajn softver Web razvoj Pretraživači i SEO Flash Javascript i AJAX Web dizajn i CSS :: Kritike Grafički dizajn Izdavaštvo 3D modelovanje Rasterska grafika Vektorska grafika 3D modelovanje :: CAD/CAM Matične ploče, procesori .. Video karte i monitori Storage Ostali hardver Overclocking & Modding PC Konfiguracije Laptopovi Vodič za kupovinu - PC har.. Tablet PC Muzička produkcija Audio kompresija Audio softver Video produkcija Video kompresija Video softver Multimedijalni uređaji Digitalni fotoaparati Digitalne kamere Home Theater Digitalni fotoaparati :: Fotografija Digitalni fotoaparati :: Vodič za kupovinu - Digita.. Elektronika Elektrotehnika Elektronika :: TV uređaji Elektronika :: Radio elektronika i tehnika Elektronika :: Mikrokontroleri Elektronika :: Audio-elektronika Auto-elektronika :: Tuning Vodič za učenje Vodič za posao Vodič za emigraciju Fizika Matematika Nauka Sertifikati Informatika Vodič za učenje :: Seminarski radovi Vodič za učenje :: Obrazovne institucije Vodič za emigraciju :: Život u USA Vodič za emigraciju :: Život u Norveškoj Vodič za emigraciju :: Život u Nemačkoj E-Poslovanje E-Kupovina IT pravo i politika razvoja IT događaji IT berza poslova IS i ERP Ekonomija Berza Cryptocoins IT berza poslova :: Arhiva IT berze poslova IT pravo i politika razvoja :: Registar Nacionalnog ID E-Poslovanje :: E-Transakcije E-Poslovanje :: Forex E-Kupovina :: Platne kartice Digitalna Televizija Advocacy Ankete Predlozi i pitanja Vesti Čekaonica Vesti :: ES leto manifestacija MadZone TechZone Poljoprivreda AutoZone MotoZone Svakodnevnica Video igre MadZone :: Zanimljivi linkovi MadZone :: Kultura TechZone :: Ergonomija TechZone :: Grejanje TechZone :: Klimatizacija TechZone :: Bela tehnika AutoZone :: Fiat Panda club Lista poslednjih: 16, 32, 64, 128 poruka.

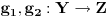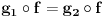pitomir Beograd Član broj: 268651 Poruke: 106 *.dynamic.isp.telekom.rs. +3 Profil Zadatak iz funkcija - dokazivanje ekvivalencije 21.08.2012. u 09:49 - pre 154 meseci Pokazati da je funkcija "na" ako i samo ako za bilo koji skup Z i bilo koje dve funkcije iz sledi 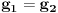. Direktan smer sam dokazala, ali za suprotan nisam sigurna. Pokusala sam da pretpostavim suprotno: f nije "na", tj. postoji 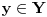tako da za svako 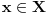, 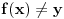. Posto vazi za svaki skup Z i svake dve funkcije g1, g2, onda recimo uzmem 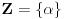. Zatim biram 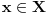proizvoljno. Onda je 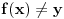, pa je 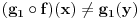, a oni valjda oba moraju biti jednaki alfa, jer i g1 i 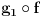slikaju u Z, koji ima samo alfu. I valjda je to kontradikcija. Jedino sto nisam iskoristila cinjenicu da iz 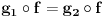sledi 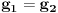, tako da mislim da mi ne valja dokaz. Moze li neko da mi pomogne? Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 *.3gnet.mts.telekom.rs. +2801 Profil Re: Zadatak iz funkcija - dokazivanje ekvivalencije 21.08.2012. u 10:06 - pre 154 meseci Iz ne sledi da jer nemaš pretpostavku o injektivnosti . Ako skup Z ima samo jedan element, postoji samo jedno preslikavanje iz Y u njega, pa sa njime nećeš ništa uraditi. Izaberi skup Z sa bar dva elementa, preslikaj y sa g1 i g2 u različite elemente skupa Z (što je moguće ako ima bar dva elementa), a sve ostale elemente skupa Y preslikaj sa g1 i g2 na isti način. Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

pitomir Beograd Član broj: 268651 Poruke: 106 *.dynamic.isp.telekom.rs. +3 Profil Re: Zadatak iz funkcija - dokazivanje ekvivalencije 21.08.2012. u 10:35 - pre 154 meseci Da, u pravu si. Evo, moze li ovako: Neka je , , . . , , pa npr. uzmem slucaj , pa je , pa g1 = g2, i to je kontradikcija, jer je alfa razlicito od beta? Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 *.3gnet.mts.telekom.rs. +2801 Profil Re: Zadatak iz funkcija - dokazivanje ekvivalencije 21.08.2012. u 11:59 - pre 154 meseci Pa, trebalo je definisati g1 i g2 i za ostale vrednosti skupa Y - na isti način. Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

pitomir Beograd Član broj: 268651 Poruke: 106 *.dynamic.isp.telekom.rs. +3 Profil Re: Zadatak iz funkcija - dokazivanje ekvivalencije 21.08.2012. u 13:28 - pre 154 meseci Aha, evo, mislim da sam se snasla. Neka je . Postoji tako da za svako , . Neka je: Neka je proizvoljno. , sledi , sto ne moze, jer . Odgovor na temu

Nedeljko Nedeljko Stefanović Član broj: 314 Poruke: 8704 *.3gnet.mts.telekom.rs. +2801 Profil Re: Zadatak iz funkcija - dokazivanje ekvivalencije 21.08.2012. u 14:12 - pre 154 meseci Da, dobro je. Moglo je i sa bilo kojim skupom Z sa bar dva elementa. Nije bitno koji su zaključci izvučeni, već kako se do njih došlo. Odgovor na temu

pitomir Beograd Član broj: 268651 Poruke: 106 *.dynamic.isp.telekom.rs. +3 Profil Re: Zadatak iz funkcija - dokazivanje ekvivalencije 21.08.2012. u 15:21 - pre 154 meseci Ok. Hvala puno! :) Odgovor na temu