Nemam pojma kako se koristi paket matematika, ali matematički gledano, radi se o problemu ekvivalentnom desetom Hilbertovom problemu.
Dokazano je da postoji polinom sa dve promenljive i realnim koeficijentima koji je nenegativan za sve realne vrednosti promenljivih, ali se ne može predstaviti kao konačan zbir kvadrata realnih polinoma.
Međutim, svaka racionalna funkcija sa realnim koeficijentima koja je nenegativna za sve realne vrednosti promenljivih za koje je definisana (za neke realne vrednosti promenljivih može biti nedefinisana) može se predstaviti kao konačna suma kvadrata racionalnih funkcija. Dakle, u opštem slučaju se nenegativan realan polinom može predstaviti kao konačan zbir kvadrata realnih racionalnih funkcija.
Najpre treba prebaciti problem u ekvivalentan oblik u kome se ne pojavljuju ograničenja promenljivih.
Primera radi, ako imamo ograničenje da je
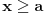
, onda treba uvesti smenu
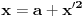
.
Ograničenje
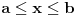
se uklanja smenom
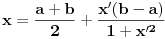
.
Ograničenje
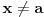
se uklanja smenom
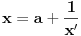
.
Kada se uklone sva ograničenja, onda je moguće primeniti neki od algoritama za rešavanje desetog Hilbertovog problema.
[Ovu poruku je menjao Nedeljko dana 23.03.2012. u 18:53 GMT+1]
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.