Citat:
igorpet: sa kojom verovatnocom mozemo tvrditi da vise ne postoji ni jedan paradoks?
Pitanje je vrlo zanimljivo i pokušaću da na njega odgovorim.
Današnja matematika je zasnovana na aksiomatskoj teoriji skupova (obično se uzima ZFC sistem), koja je zasnovana na predikatskom računu prvog reda, koji je zasnovan na svojim aksiomama i pravilima izvođenja. Dakle, imamo pravila izvođenja predikatskog računa prvog reda, aksiome predikatskog računa prvog reda i aksiome teorije skupova. Svi ostali pojmovi (osim skupa) su definisani preko pojma skupa.
Paradoks bi bio način da se po tim pravilima izvede neka formula i negacija te formule ili ekvivalentno da se dobije npr. formula
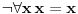
konačnom primenom pravila izvođenja predikatskog računa prvog reda na aksiome predikstskog računa prvog reda i teorije skupova. Takva (eventualna) mogućnost se zove protivrečnost teorije skupova.
Današnji matematičari (uz možda neke vrlo retke izuzetke) čvrsto veruju da je matematika neprotivrečna, odnosno da takvo izvođenje nije moguće, jer bi u protivnom menjali zasnivanje matematike. Međutim, tu neprotivrečnost niko nije dokazao prihvatljivim sredstvima. Štaviše, Kurt Gedel je dokazao da takav dokaz nije ni moguć istim takvim sredstvima, pa samim tim ni slabijim. Štaviše, dokazao je da je bilo kakav eventualni pokušaj zasnivanja matematike unapred osuđen ili na protivrečnost ili na nepotpunost uz nemogućnost dokazivosti neprotivrečnosti istim, odnosno slabijim sredstvima.
Kakve su onda perspektive za ispitivanje neprotivrečnosti zasnivanja matematike? Pa, matematičari svakoga dana dokazuju sve veći broj teorema. Ako bi paradoks postojao, postoji mogućnost da bi ga se neko setio. Međutim, to se nije desilo. To je jedna vrsta empirijske potvrde da paradoksa nema, ali naravno, ne i matematički dokaz (kakav po Gedelu nije ni moguć).
Sa druge strane, ako uz ZFC pretpostavimo postojanje slabo nedostižnih kardinala (WIC), odnosno pojačamo sredstva za dokazivanje, onda možemo da dokažemo (takvim, jačim sredstvima) da je ZFC neprotivrečan sistem.
Međutim, ko nam garantuje da je ta teorija neprotivrečna. Možda je ZFC protivrečna teorija, pa samim tim i ovakvo proširenje, pa pomenuti dokaz ne znači mnogo. Možda je pritom izvođenje protivrečnosti u ZFC toliko teško da ga se niko nije setio, ali bi onda u izvođenje kontradikcije u jačem sistemu ZFC+WIC bilo lakše. Ipak, ni izvođenja kontradikcije u tom sistemu se niko nije setio.
OK, možda je i to teško. Hipotezu o slabo nedostižnim kardinalima možemo zameniti još jačom hipotezom o postojanju jako nedostižnih kardinala (SIC), pa bi izvođenje protivrečnosti u sistemu ZFC+SIC bilo još lakše i bilo bi još lakše izvesti protivrečnost, odnosno bilo bi još izvesnije da se neko toga seti. Međutim, ni toga se niko nije setio.
Ako SIC zamenimo hipotezom o postojanju merljivih kardinala (MC), onda možemo dokazati da je ZFC+SIC neprotivrečna teorija. No, onda bi i ZFC+MC bila protivrečna teorija sa još lakšim načinom dolaženja do kontradikcije, jer smo pojačali sredstva, pa bi bilo još verovatnije da bi se neko setio takvog izvođenja kontradikcije. Međutim, ni toga se niko nije setio.
E, sad, postoje još veći tipovi kardinala u smislu da postojanje kardinala većeg tipa povlači da postoji ispod njega kardinal manjeg tipa, odakle sledi da se postojanje većeg povlači neprotivrečnost teorije skupova sa postojanjem manjeg kardinala. Postoji desetine tipova kardinala u toj hijerarhiji. Ni uz pretpostavku postojanja najvećih od njih niko još nije uspeo da izvede kontradikciju, što znači da je "običan" ZFC najverovatnije stvarno neprotivrečan.
U svakom slučaju, ako neko i pronađe protivrečnost unutar nekog od tih sistema, to neće biti nivo euklidske, pa ni neeuklidskih geometrija, jer je taj deo vrlo čvrsto zasnovan preko realnih brojeva, koji se na kraju zasnivaju preko prirodnih, već će se takva (eventualna) protivrečnost nalaziti u mnogo apstraktnijim slojevima.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.