Neka je
neprazan skup (zvaćemo ga skupom vektora) i neka je data binarna operacija
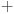
nad elementima tog skupa, koja ima uobičajene osobine, kao npr. sabiranje realnih brojeva. Recimo, postoji neuralni element i svakom elementu postoji suprotan, tako da elementa u zbiru sa svojim suprotnim elementom daje neutralni element i neka važe zakoni
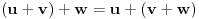
i
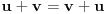
. Preciznije, pretpostavlja se da za elemente tog skupa važe sledeći zakoni:
,
,
,
,
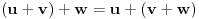
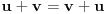
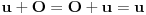
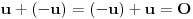
gde smo sa
označili neutralni element (koji uzgred pripada skupu
), a sa
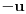
suprorotan element od elementa
. Neka je data i operacija množenje vektora realnim (odnosno kompleksnim) brojevima tako da ako brojeve označimo grčkim, a vektore latiničnim slovima, važe sledeći zakoni
,
,
,
.
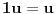
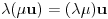
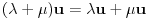
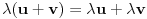
Tada kažemo da je skup
snabdeven ovim operacijama realan (odnosno kompleksan) vektorski prostor.
Ako je pritom data jedna binarna operacija
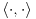
koja parovima vektora pridružuje realne (odnosno kompleksne) brojeve (koje zovemo i skalarima) tako da su ispunjeni sledeći uslovi:
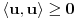
(dakle,
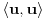
mora biti realan nenegativan broj, čak i ako smo uzeli kompleksne brojeve kao skalare).
Ako je
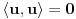
, onda je
.
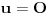
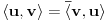
("nadvučeno" je ovde oznaka za kompleksni konjugat. U realnom slučaju se to naravno svodi na
,
.
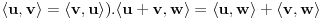
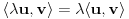
Za
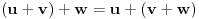
i
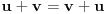
Tada takvu operaciju zovemo skalarnim proizvodom.
Za vektore se kaže da su ortogonalni ako im je skalarni proizvod jednak nuli. Ako je
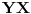
sistem uzajamno ortogonalnih vektora, među kojima se ne nalazi
i
bilo koji vektor, se za broj
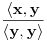
kaže da je Furijeov koeficijent vektora
po vektoru
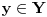
, a za formalan red
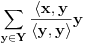
da je Furijeov red vektora
po sistemu
.
U svakom slučaju,
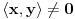
za najviše prebrojivo mnogo
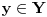
i pritom je
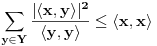
. To je Beselova nejednakost. Pritom jednakost važi za sve moguće vektore
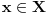
ako i samo ako je
maksimalan ortogonalan podskup od
(koji ne uključuje
).
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.
Furijeovi brojevi i beselova nejednakost
