Citat:
westocean:
Postavljeno pitanje je veoma zanimljivo. Ako se reprezentacija brojeva proširi na neke nestandardne osnove tada neki prirodni brojevi ne bi morali da imaju konačan broj cifara.
Možeš li prevesti neki prirodan broj iz dekadnog brojnog sistema u brojni sistem sa nekom drugom osnovom tako da njegov zapis u tom brojnom sistemu ima beskonačno mnogo cifara (primjera radi može i u brojni sistem sa osnovom
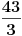
)?
Citat:
Nedeljko:
A u čemu je problem sa ovim načinom?
Ni u čemu.
Zanima me može li da se dokaže na neki drugi način bez pozivanja na princip matematičke indukcije?
Citat:
Nedeljko:
Osnova može biti bilo koji kompleksan broj, a skup cifara može biti bilo koji skup kompleksnih brojeva. Na srpskom jeziku nešto o tome možeš naći u knjizi "Realni brojevi" Milojice Jaćimovića. Recimo, Knut je dokazao da se svaki kompleksan broj može prikazati na jedinstven način u sistemu sa osnovom 1-i sa skupom cifara {0,1}.
Ima li išta od toga u elektronskom obliku na srpskom jeziku da se može naći na internetu?